Wellen treten dann immer auf, wenn sich eine physikalische Größe zeitlich und räumlich periodisch ändert. Dies ist auch bereits der wesentliche Unterschied zwischen einer Welle und einer Schwingung. Schwingungen sind periodisch bezüglich der Zeit, während Wellen periodisch bezüglich Raum und Zeit sind. Beispiele für mechanische Wellen sind Wasserwellen und Schallwellen
Für die Herleitung der Wellengleichung wird also die Formel für die Auslenkung eines (einzelnen) harmonischen Oszillator verwendet. Die räumliche, periodische Bewegung im Raum wird durch eine Sinuskurve beschrieben.
Herleitung der Wellengleichung für mechanische Wellen (Sek 1 – Niveau)
Zur Erinnerung: Wichtige Größen zur Beschreibung einer mechanischen Welle sind die Amplitude, die Frequenz und die Wellenlänge:
Wie eingangs erwähnt, ist die Grundlage / Entstehung einer Welle ein schwingender Oszillator. Damit diese Schwingung zur einer Welle führt, muss diese Schwingung harmonisch (also gleichmäßig) und periodisch sein.
Im Allgemeinen wird eine periodische zeitabhängige Bewegung durch eine Winkelfunktion (Sinus oder Cosinus-Funktion) beschrieben. Betrachten wir uns nun eine Welle, so sieht diese wie eine Sinus-Funktion aus:

Für die Bewegung können wir also schreiben: y = y(max)·sin (x). Eine Wellenbewegung können wir auch als kreisförmige Bewegung sehen.
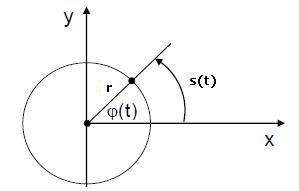
Die Strecke s bzw. x, die ein Körper in der Zeit t auf der Kreisbahn zurücklegt, ist definiert als das Produkt aus Winkelgeschwindigkeit w und Zeit t (x = w · t)
Somit erhalten wir für die zeitabhängige Auslenkung eines harmonischen Oszillators
folgende Gleichung: y(t) = y(max)·sin (w · t)
Nun denken wir an die Einführung zurück, wie sich eine Welle ausbreitet. Ein Oszillator, der in einer Entfernung x vom schwingenden Oszillator (= Erreger) entfernt ist, wird erst nach einer gewissen Zeit zum Schwingen angeregt (das kennt man auch von Wasserwellen, man kann zusehen, wie sie sich ausbreiten).
Die Gleichung für diesen Oszillator lautet damit: y(t) = y(max)·sin (w · [t – t(x)])
Gemäß den Newtonschen Axiomen gilt: Zeit = Strecke : Geschwindigkeit bzw. in unserem Fall Zeit t = Strecke x : Ausbreitunngsgeschwindigkeit c => t = x : c. Weiterhin wissen wird, dass die Ausbreitungsgeschwindigkeit c einer Welle folgendermaßen definiert ist:


Setzen wir dies nun in die Wellengleichung ein, erhalten wir:

Meistens wird in der Gleichung die Winkelgeschwindigkeit w durch andere Größen wie die Umlaufdauer T ersetzt. Damit erhalten wir nun für die Auslenkung einer Welle an einem Ort x zum Zeitpunkt t(x) folgende Gleichung:

Ein Phänomen, bei dem Energie durch eine Materie getragen wird, ohne dass die Materie selbst transportiert wird, heißt als mechanische Welle.
Mechanische Wellen benötigen ein Medium zur Ausbreitung; sie können sich durch Festkörper, Flüssigkeiten und Gase ausbreiten.
Bei Longitudinalwellen ist die Schwingungsrichtung parallel zur Ausbreitungsrichtung der Welle. Bei Transversalwellen ist die Schwingungsrichtung senkrecht zur Ausbreitungsrichtung.
Die Wellengleichung ist eine partielle Differentialgleichung, die die Ausbreitung von Wellen beschreibt.
Die Wellenformel in einem-dimensionalen Raum lautet: ∂²u/∂t² = c² * ∂²u/∂x².
Die Amplitude einer Welle ist der maximal mögliche Auslenkung der Wellenpartikel von ihrer Ruhelage und gibt somit die Energie der Welle an.
Die Geschwindigkeit einer mechanischen Welle wird durch das Medium und seine Eigenschaften bestimmt.
Eine stehende Welle ist das Resultat der Überlagerung zweier gleichartiger Wellen derselben Amplitude und Frequenz, die sich in entgegengesetzten Richtungen bewegen.
Die Wellenfront ist die Linie oder Fläche, die alle Punkte verbindet, die sich in der gleichen Phase der Welle befinden.
Unter Interferenz versteht man das Phänomen der Überlagerung von Wellen, bei dem es zu Verstärkung (Konstruktive Interferenz) oder Abschwächung (Destruktive Interferenz) der Amplitude kommen kann.