Im Allgemeinen versteht man unter Beugung (manchmal auch als Diffraktion bezeichnet) die Ablenkung von “Wellen” an einem Hindernis. Die Beugung von geradlinigen Ausbreitung von Wellen (Wellen können u.a. Wasser-, Schall-, Lichtwellen sein) tritt auf, wenn die Welle auf einen Gegenstand trifft oder durch einen Spalt “geht”. Die Beugung kann nach dem Huygensschen Prinzip beschrieben werden.
Wie bereits in der Einleitung erwähnt, tritt die Lichtbeugung auf, wenn Licht auf ein Hindernis trifft, dies sind Einzelspalt, Doppelspalt und Mehrfachspalt (Gitter).
Nachfolgend soll die Lichtbeugung an einem Einzelspalt erklärt werden.
Wie in dem allgemeinen Teil über Lichtstreuung, Lichtbrechung und Lichtbeugung erklärt, liegt eine Lichtbeugung vor, wenn eine Wellenfront auf einen Spalt trifft, und nach dem Huygen’schen Prinzip jeder Punkt der Wellenfront der Ausgangspunkt einer neuen Welle ist, so dass ein Interferenzmuster (Minima und Maxima) entsteht, dass gemessen werden kann.
Wie bereits im Kapitel “Lichtbeugung” erklärt, sollte man die Begriffe “Beugung” und “Interferenz” unterscheiden, obwohl beide Begriffe im Grunde das gleiche Phänomen erklären. So kann man sich merken
Die Lichtbeugung kommt so zustande, indem eine Lichtwelle auf einen Einfachspalt trifft. Dabei kommt es zur Beugung an diesem Spalt und hinter dem Spalt bildet sich nach dem Huygen´schen Prinzip eine neue Wellenfront. Diese Elementarwellen breiten sich hinter dem Spalt in alle Richtungen gleichmäßig aus und überlagern sich dabei. Durch dieses Elementarwellen kommt es zu konstruktiver Interferenz (Maxima) und destruktiven Interferenz (Minima), dass ein typisches Interferenzmuster erzeugt.
Die Schnittpunkte der Wellenfronten ergeben eine Intensitätsverstärkung, die sog. Maxima (mit unterschiedlichen Ordnungen). Zwischen diesen Intensitätsmaxima liegen die Intensitätsminima, wobei der Phasenunterschied zwischen den beiden interferierenden Wellen eine halbe Wellenlänge beträgt.

Erklärung:
Bis zum Hauptmaximum haben beide Wellenfronten (nach dem Spalt) dieselbe Weglänge zurückzulegen und sind daher phasengleich (= Wellenberg trifft auf Wellenberg bzw. Wellental auf Wellental), was zu einer konstruktiven Überlagerung führt und dabei ein Maximum entsteht. Links und rechts nahe am Maximum, ist die Überlagerung der beiden Wellenfronten nicht mehr exakt phasengleich (unterschiedliche Weglänge), dennoch tritt immer noch Verstärkung auf. Geht man noch weiter links und rechts vom Maximum weg, so wird die Verstärkung immer geringer und geht ab einem gewissen Punkt in eine Abschwächung über, bis sich im Falle einer Phasenverschiebung von 180° ein Minimum ergibt (Wellenberg und Wellental addieren sich).
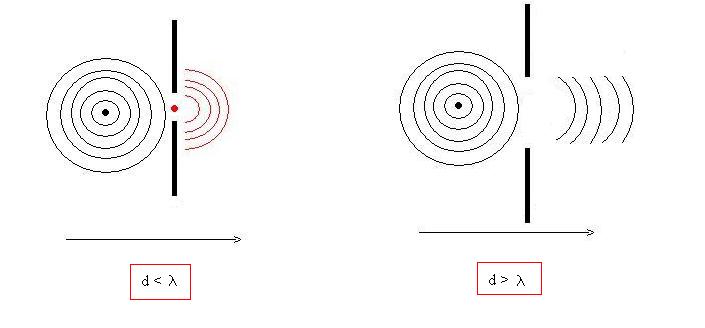
Unter Lichtbeugung versteht man die Abweichung des Geradeauslaufes des Lichts, die auftritt, wenn eine Lichtwelle an einem Hindernis oder einer Öffnung vorbeiläuft. Das Phänomen wird durch die Welleneigenschaft des Lichts erklärt.
Wenn Licht auf einen Einzelspalt fällt, beugt es sich an den Rändern des Spalts ab und erzeugt ein Interferenzmuster auf dem hinter dem Spalt befindlichen Schirm. Dieses Muster besteht aus einem hellen Zentralmaximum und dunklen Minima, abwechselnd mit weniger hellen Maxima.
Interferenzmuster sind Muster von hellen und dunklen Bereichen, die durch die Interferenz von Lichtwellen erzeugt werden. Sie entstehen, wenn die Wellen aus zwei Quellen an verschiedenen Stellen überlagert werden und sich verstärken oder auslöschen.
Das Zentralmaximum ist die Mitte des Interferenzmusters, die durch die Lichtbeugung an einem Einzelspalt entsteht. Es ist der hellste Bereich des Musters und wird durch die konstruktive Überlagerung der Lichtwellen erzeugt.
Die Größe des Spalts und die Wellenlänge des Lichts sind die Hauptfaktoren, die die Breite und Intensität des Zentralmaximums beeinflussen. Eine kleinere Spaltbreite oder eine größere Wellenlänge führt zu einer breiteren Beugungsfigur und einem weniger intensiven Zentralmaximum.
Das Beugungsbild setzt sich aus einem zentralen hellen Streifen (Zentralmaximum), umgeben von mehreren schwächeren hellen Streifen (Nebenmaxima) zusammen. Dazwischen befinden sich dunkle Streifen (Minima), an welchen sich die Lichtwellen destruktiv überlagern.
Wenn die Wellenlänge des Lichts verändert wird, verändert sich das Beugungsmuster. Eine größere Wellenlänge führt zu einem breiteren Beugungsmuster und einer geringeren Ortsfrequenz der Maxima und Minima.
Die Größe des Spalts beeinflusst die Breite des Beugungsmusters. Ein kleinerer Spalt führt zu einem breiteren Beugungsmuster und einem weniger scharfen Zentralmaximum.
Bei konstruktiver Interferenz verstärken sich die Wellen, wodurch helle Bereiche (Maxima) im Interferenzmuster entstehen. Bei destruktiver Interferenz löschen die Wellen einander aus, wodurch dunkle Bereiche (Minima) im Muster entstehen.
Der fundamentale Unterschied liegt in der Dualität von Welle und Teilchen in der Quantenphysik. Während Licht sowohl Teilchen- als auch Welleneigenschaften zeigt (Wellenteilchendualismus), verhalten sich Materieteilchen in der klassischen Physik nicht wie Wellen. Daher zeigt Licht Beugung, während klassische Teilchen sich geradlinig bewegen.