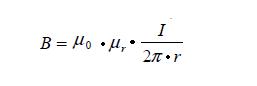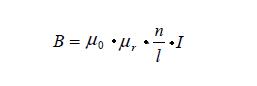Hans Christian Oerstedt entdeckte im 19. Jahrhundert, dass ein stromdurchflossener Draht von einem Magnetfeld mit konzentrischen Feldlinien umgeben ist. Die Richtung der Feldlinien ist dabei von der Stromrichtung (durch den Draht) abhängig. Dies führte zur Erkenntnis dass Magnetfelder ausschließlich durch Ladungstransport (von Ladungen) erzeugt werden. Daher stehen Magnetfelder und elektrische
Ströme in einem ursächlichen Zusammenhang.
Magnetfelder
In einem anderen Kapitel auf Lernort-mint wurde erläutert, wie elektrische Felder entstehen. Ähnlich wie bei den Ladungsträgern spricht man beim Phänomen Magnetismus ebenfalls von Magnetfelder. Zur Angabe der Stärke eines Magnetfeldes gibt man die sog. magnetische Flussdichte B an. Die Formel für die magnetische Flussdichte lautet:

In der oben abgebildeten Formel kommen zwei Werte für die Permeabilität vor, da das Magnetfeld in der Regel in Materie erzeugt wird und nicht im Vakuum. Magnetfelder haben stets geschlossene Feldlinien, und sind stets Dipole (Nord- und Südpol)
Magnetfelder von geradlinigen Leitern
Wie bereits beschrieben, erzeugt ein stromdurchflossener (geradliniger) Leiter ein Magnetfeld, dabei sind die Magnetfeldlinien konzentrische Kreise um den Leiter. Die Flussdichte läßt sich hierbei aus der konstanten Stromstärke I und dem Abstand r zum Leiter berechnen. Jeder kennt bestimmt die Regel, um die Lage des Magnetfeldes zu bestimmen: Umfasst man den Leiter mit der rechten Hand, so dass der ausgestreckte Daumen in Richtung der Stromrichtung zeit, so zeigen die um den Leiter gekrümmten Finger die Richtung des Magnetfeldes an. Formelmäßig gilt:
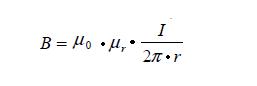
Magnetfeldern von Leiterschleifen
Wie bereits erwähnt, wird ein geradliniger Leiter von konzentrischen magnetischen Feldlinien umgeben. Hat man nun eine Leiterschleife (also eine Spule), so haben die Feldlinien eine ähnliche Form, wie bei einem Stabmagneten. Im Spuleninneren verlaufen die Feldlinien nahezu parallel. Das magnetische Feld einer langen Spule, bei der eine Überlagerung der Felder vieler Leiterschleifen stattfinden, lässt sich teilweise recht einfach berechnen. Die Feldstärke im Innern der Spule mit der Länge l, der Windungszahl n und der Stromstärke I kann durch folgende Formel berechnet werden:
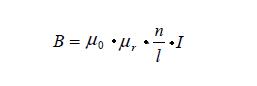
Magnetfelder – Testfragen/-aufgaben
1. Was ist ein Magnetfeld?
Ein Magnetfeld ist eine Region um ein magnetisches Material oder einen bewegenden elektrischen Strom, innerhalb derer magnetische Kräfte beobachtet werden können.
2. Was repräsentiert die Richtung der Magnetfeldlinien?
Die Richtung der Magnetfeldlinien repräsentiert die Richtung, in die eine Nordspitze eines Kompasses weisen würde, wenn sie an dem Punkt platziert würde.
3. Wovon hängt die Stärke eines Magnetfelds ab?
Die Stärke eines Magnetfelds hängt von der Menge des magnetischen Materials und der Entfernung von der Quelle ab.
4. Wie heißen die beiden Pole eines Magneten?
Die beiden Pole eines Magneten heißen Nordpol und Südpol.
5. Was passiert, wenn man einen Magneten halbiert?
Wenn man einen Magneten halbiert, erhält man zwei kleinere Magneten, jeweils mit einem Nordpol und einem Südpol.
6. Können Magnetfeldlinien sich kreuzen?
Nein, Magnetfeldlinien können sich nicht kreuzen.
7. Was ist der Unterschied zwischen einem homogenen und einem inhomogenen Magnetfeld?
Ein homogenes Magnetfeld hat in jedem Punkt dieselbe Stärke und Richtung, während ein inhomogenes Magnetfeld in verschiedenen Punkten unterschiedliche Stärken und/oder Richtungen aufweist.
8. Wie äußert sich die magnetische Kraft auf bewegte Ladungen?
Die magnetische Kraft auf bewegte Ladungen äußert sich als Ablenkung ihrer Bewegungsbahn.
9. Was hat die Erde mit Magnetfeldern zu tun?
Die Erde besitzt ein eigenes Magnetfeld, ähnlich dem eines Stabmagneten mit Nord- und Südpol.
10. Was ist magnetischer Fluss?
Der magnetische Fluss ist ein Maß für die Menge des Magnetfelds, das eine bestimmte Fläche durchdringt. Er wird in der Einheit Weber gemessen.