Die Zentripetalkraft ist eine Kraft, die einen bewegten Körper auf einer Kreisbahn hält. Ohne die Zentripetalkraft würde der Körper die Kreisbahn tangential verlassen. Die Richtung der Zentripetalkraft zeigt immer zum Kreismittelpunkt.
Definitionsgemäß verlaufen die Geschwindigkeitsvektoren bei einer Kreisbewegung immer tangential zur Kreisbahn und stehen immer senkrecht zum Radius(vektor).
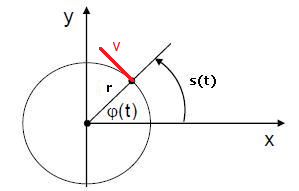
Wie eingangs erwähnt, ist die Zentripetalkraft die Kraft, die dafür sorgt, dass sich ein Körper auf einer Kreisbahn bewegt, ohne das der Körper die Kreisbahn verlässt.
Die Zentripetalkraft (bzw. die Formel zur Berechnung der Zentripetalkraft kann einfach mit Hilfe des 2.Newtonschen Gesetzes “hergeleitet” werden. Für eine Kraft gilt allgemein: F = m · a (= Masse x Beschleunigung). Dies gilt auch für die Zentripetalkraft beziehungsweise für die Zentrifugalbeschleunigung.
Fz = m · a = m · (v² : r) = m · w² · r
(mit w = Winkelgeschwindigkeit, r = Bahnradius, m = Masse des Körpers auf der Kreisbahn).
Mit Hilfe dieser Formel können wir einige Aussagen über die Zentripetalkraft treffen (die im ersten Moment vielleicht widersprüchlich klingen):
Zentripetalkraft und Energieerhaltung:
Zur Erinnerung: Bei der gleichförmigen Kreisbewegung handelt es sich um eine beschleunigte Bewegung. Bei der Kreisbewegung bleibt zwar der Wert (der Betrag) der Geschwindigkeit konstant, aber die Richtung des Geschwindigkeitsvektors ändert sich ständig. Eine Änderung der Geschwindigkeit bzw. des Geschwindigkeitsvektors ist nur möglich, wenn sich die Beschleunigung bzw. die Richtung der Beschleunigung ständig ändert.
Betrachten wir nun eine horizontale verlaufende Kreisbahn (kein Höhenunterschied auf der Kreisbahn). Daher betrachten wir in diesem Fall nur die kinetische Energie E = 0,5 · m ·v² (Bewegungsenergie). Während der Bewegung eines Körpers auf einer Kreisbahn ändert sich die kinetische Energie nicht, obwohl wir wissen, dass auf die Bewegung ständig eine Kraft (Zentripetalkraft) wirkt. Dies kommt daher, dass sich während der Kreisbewegung nur die Richtung des Geschwindigkeitsvektors ändern, nicht aber der Wert/Betrag der Geschwindigkeit.
Dies können wir einfach mathematisch bzw. physikalisch begründen. Die Zentripetalkraft steht immer senkrecht zur Bewegungsrichtung. Aus der Mechanik wissen wir, dass eine Energieänderung berechnet werden kann durch die Streckenlänge, auf die die Kraft wirkt DE = F ·Ds· cos(a) (wobei D = Delta = Differenz). Bei der Kreisbewegung ist der Winkel a 90° (senkrecht zur Bewegungsrichtung). Da gilt cos(90°) = 0, gilt DE = 0, also keine Änderung in der kinetischen Energie während einer Kreisbewegung.
——————————————————————————————————————————-
Ergänzung zur Zentripetalkraft : warum gilt v = w· r
