Die gleichmäßig beschleunigte Bewegung

In der Mechanik ist es Ziel, neben den Kräften in einem System auch die Bewegungen von Körpern zu beschreiben, da die Bewegungen meist auch mit Kräften zu tun haben.Begonnen wird immer mit der einfachsten der Bewegungen, der so genannten gleichförmigen Bewegung. Neben der gleichförmigen Bewegung gibt es noch die gleichmäßig beschleunigte Bewegung:

Die gleichmäßige beschleunigte Bewegung

Definitionsgemäß liegt eine gleichmäßige beschleunigte Bewegung vor, wenn

• Die Geschwindigkeit eines Körpers sich ändert, d.h. der Körper wird entweder schneller oder langsamer.
• Die Beschleunigung a ist ungleich Null.
• Die Beschleunigung ist bei einer gleichmäßig beschleunigten Bewegung immer konstant

Herleitung der Formel

Die Formel zur Berechnung der gleichmäßig beschleunigten Bewegung setzt die Größen Strecke v(t), Beschleunigung a, Zeit t, Anfangsgeschwindigkeit v_o und Anfangsweg s_o in Relation zueinander. Daraus kann man zwei Formeln ableiten:

Geschwindigkeits-Zeit-Gesetz:

Hinweis / Verweis auf weitere Kapitel

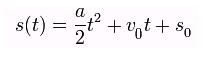
Die Geschwindigkeit ist eine vektorielle Größe, die durch den Betrag (= Größe) und der Richtung “definiert” ist. Daher liegt auch eine Beschleunigung vor, wenn sich die Richtung der Bewegung des betrachteten Körpers ändert. Daher sind Kreisbewegungen auch beschleunigte Bewegungen. Dies wird unter anderem auch durch das Vorliegen der “zentripetalen Beschleunigung” deutlicht.

Daher gilt: Eine Beschleunigung liegt auch dann vor, wenn sich ein Körper auf einer gekrümmten Bahn mit gleichbleibender “Geschwindigkeit” bewegt.

Die gleichmäßig beschleunigte Bewegung – Testfragen/-aufgaben

1. Was bedeutet der Begriff “gleichmäßig beschleunigte Bewegung”?

Eine gleichmäßig beschleunigte Bewegung ist eine Bewegung, bei der die Geschwindigkeitsänderung pro Zeiteinheit (Beschleunigung) konstant ist.

2. Wie kann die gleichmäßig beschleunigte Bewegung berechnet werden?

Die gleichmäßig beschleunigte Bewegung kann mit der Formel v = u + at berechnet werden, wobei v die Endgeschwindigkeit, u die Anfangsgeschwindigkeit, a die Beschleunigung und t die Zeit ist.

3. Was passiert, wenn die Beschleunigung bei einer gleichmäßig beschleunigten Bewegung negativ ist?

Wenn die Beschleunigung negativ ist, spricht man von einer gleichmäßig verzögerten Bewegung. Das Objekt verlangsamt sich also im Laufe der Zeit.

4. Wie berechnet man die zurückgelegte Strecke bei einer gleichmäßig beschleunigten Bewegung?

Die zurückgelegte Strecke kann mit der Formel s = ut + 0.5at^2 berechnet werden, wobei s die Strecke, u die Anfangsgeschwindigkeit, a die Beschleunigung und t die Zeit ist.

5. Wie verhält sich das Geschwindigkeits-Zeit-Diagramm bei einer gleichmäßig beschleunigten Bewegung?

Bei einer gleichmäßig beschleunigten Bewegung ergibt sich im Geschwindigkeits-Zeit-Diagramm eine gerade Linie, die gegen die Zeitachse aufsteigt.

6. Was ist der Unterschied zwischen einer gleichmäßigen und einer gleichmäßig beschleunigten Bewegung?

Bei einer gleichmäßigen Bewegung bleibt die Geschwindigkeit konstant, während bei einer gleichmäßig beschleunigten Bewegung die Geschwindigkeit kontinuierlich ansteigt oder abnimmt.

7. Welche Einheit hat die Beschleunigung in der Physik?

Die Einheit der Beschleunigung ist Meter pro Quadratsekunde (m/s²).

8. Was ist das besondere an einer gleichmäßig beschleunigten Bewegung in der Physik?

Das Besondere an einer gleichmäßig beschleunigten Bewegung ist, dass sie durch ihre konstante Beschleunigung charakterisiert ist und deshalb in der realen Welt eher selten vorkommt, da die meisten Bewegungen durch Reibung und andere Faktoren beeinflusst werden.

9. Wie berechnet man die Endgeschwindigkeit bei einer gleichmäßig beschleunigten Bewegung, wenn die Anfangsgeschwindigkeit und die Beschleunigung gegeben sind?

Die Endgeschwindigkeit wird durch die Formel v = u + at berechnet. Wenn die Anfangsgeschwindigkeit u und die Beschleunigung a gegeben sind, kann die Endgeschwindigkeit v nach einer bestimmten Zeit t gefunden werden.

10. Was passiert mit der Formel für die gleichmäßig beschleunigte Bewegung, wenn die Anfangsgeschwindigkeit null ist?

Wenn die Anfangsgeschwindigkeit null ist, reduziert sich die Formel für die gleichmäßig beschleunigte Bewegung auf v = at und die Formel für die zurückgelegte Strecke auf s = 0.5at^2.