Jede Ladung erzeugt ein Feld (ähnlich einer Masse). Dies lässt sich in einem Vergleich veranschaulichen: Jede Masse erzeugt ein Schwerefeld um sich herum erzeugt (z.B. bei der Erde als Erdbeschleunigung), so bewirkt auch jede elektrische Ladung ein elektrisches Feld, dass in alle Richtungen gerichtet ist, wofür folgende Formel verwendet werden kann:
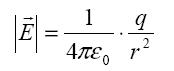
Nun wollen wir uns das elektrische Potential als physikalische Größe betrachten und werden bemerken, dass die beiden “Größen” elektrisches Feld und elektrisches Potential zusammenhängen.
Wie in der Einleitung gezeigt, beschreibt das elektrische Feld die Kraft, die auf eine sogenannte Probeladung q wirkt. Diese (gerichtete) Kraft ist abhängig von der Ladung der Probeladung bzw. des Probekörpers, d.h. die Kraft, die wir als Ergebnis erhalten ist abhängig von der Ladung.
Genau dies macht man auch beim Übergang vom elektrischen Feld zum elektrischen Potential. Man beschreibt hierbei ein elektrisches Feld bzw. eine Kraft, die unabhängig von der Ladung ist, die im elektrischen Feld bewegt wird. Das elektrische Potential hängt dann nur noch vom Ort r ab (und nicht mehr von der Ladung). Dieses elektrische Potential wollen wir nun herleiten:
Dazu stellen wir uns ein elektrisches Feld vor (z.B. in einem Plattenkondensator). In dieses elektrische Feld bringen wir nun eine Probeladung, die positiv geladen ist. Durch das elektrische Feld wirkt nun eine Kraft auf die Probeladung, die positive Probeladung wird von der negativ geladenen Platte des Kondensators angezogen. Will man nun die Probeladung in dem elektrischen Feld verschieben (gegen die Anziehung durch die negativ geladene Platte) muss Energie aufgewendet werden. Man muss Arbeit verrichten, da die Ladung gegen das elektrische Feld verschoben wird. Durch die Verrichtung der Arbeit an der Probeladung erhält die Ladung eine bestimmte Menge an potentieller Energie (analog: bei Bewegung (Anheben) einer Masse entgegen dem Schwerefeld, der Massekörper gewinnt an potentieller Energie, die z.B. frei wird, wenn man den Körper fallen lässt).
Somit könnte man nun das elektrische Potential (im Sinne einer potentiellen Energie) herleiten, aus dem Produkt aus Kraft und Weg (wie in der Physik üblich). Damit hätten wir als Formel für das elektrische Potential E(pot) = F · s (mit F = q · E) bzw. E(pot) = q · E ·s
Ähnliche Situationen haben wir auch in allen anderen naturwissenschaftlichen Fächern, beispielsweise dem Erwärmen von Wasser. Wenn wir eine Menge Wasser erwärmen, benötigen wir hierzu eine bestimmte Menge (Wärme)energie. Würden wir nun sagen, wir hätten 500 J benötigt,um das Wasser zum Sieden zu bringen, wäre das sicher eine richtige Aussage, aber nicht vollständig. Geben wir aber z.B. die spezifische Wärmekapazität an (z.B 4,2 Joule pro Gramm und Kelvin) so können wir den ganzen Vorgang nachvollziehen
Daher wird als elektrische Potential als potentielle Energie pro Ladung definiert:
φ(r)=E(pot) : q = q · E · s : q = E ·s
Damit erhalten wir eine Aussage über die potentielle Energie einer Probeladung in einem elektrischen Feld, die aber normiert ist, nämlich als potentielle Energie pro Ladung. Das elektrische Potential ist also die potentielle Energie an einem bestimmten Punkt eines elektrischen Feldes. Das elektrische Potential entspricht der Arbeit, die aufgewendet werden muss, um eine Ladung im elektrischen Feld zu bewegen.