Im Allgemeinen ist die Integralrechnung die Umkehrung der Differenzialrechnung (Integration ist die Umkehr der Ableitung): Der Zusammenhang zwischen Integral (wird als Stammfunktion F(x) bezeichnet) und “Ableitung” f(x) lautet: F(x) + C = ∫ f(x) dx und F'(x) = f(x).
Die Integration bzw. die Integralbildung einer Funktion diente ursprünglich zur Bestimmung eines Flächeninhaltes unterhalb eines Funktionsgraphens (zwischen Graph und x-Achse). Dieser Flächeninhalt (das sogenannte bestimmte Integral) ist heute in der Mathematik eher von untergeordneter Bedeutung. Meistens will man heute das unbestimmte Integral einer Funktion (= die Stammfunktion) bestimmen. Eine Funktion (die Stammfunktion als unbestimmtes Integral) bietet mehr Möglichkeiten (=> Kurvendiskussion), als nur die einfache Betrachtung eines Wertes (Flächeninhalt, bestimmte Integral)
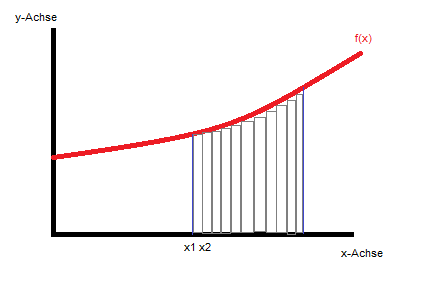
Das Integral wurde (eigentlich) entwickelt, um den Flächeninhalt unter einem Graphen zu ermitteln. Dazu folgendes Beispiel: Wir betrachten und den Graphen der Funktion f(x) (in der Abbildung rot dargestellt). Nun möchten wir gerne wissen, welchen Flächeninhalt sich unter dem Graphen (jeweils bis zur x-Achse) befindet. Dazu hat man den Flächeninhalt (in der Abbildung durch die blauen und rote Linien eingegrenzt) in möglichst viele Rechtecke unterteilt.
Integralrechnung in der Mathematik
Der Vorteil eines Rechtecks: Der Flächeninhalt kann einfach berechnet werden, nämlich aus Länge x Breite. In unserem Fall entspricht die Bereite der Differenz zwischen zwei x-Werten (z.B. Δx = x2 – x1). Die Höhe unseres Rechtecks entspricht (etwa) dem Funktionswert (= y-Wert) an der Stelle x1. Daher kann man nun den Flächeninhalt unter dem Graphen folgendermaßen ermitteln:
Fläche = f(x1)·(x2-x1) + f(x2)·(x3-x2) + f(x3)·(x4-x3) + ………….
Fläche = Σ f(xi)·Δx
Vergleicht man nun das Integral einer Funktion lässt sich die ehemalige Verwendung eines Integrals deutlich erkennen
F = ∫ f(x)·dx (d steht für Differential, also unendlich keine Δ)
Heute kennt man zwei Arten von Integralen, das bestimmte und das unbestimmte Integral. Das bestimmte Integral entspricht dem Flächeninhalt unter einem Graphen zwischen zwei x-Werten. Das unbestimmte Integral hingegen ist eine Funktion (und kein Zahlenwert). Das unbestimmte Integral einer Funktion wird als die Stammfunktion bezeichnet der ursprünglichen Funktion bezeichnet.
Eine Funktion ist integrierbar, wenn sie in dem Bereich, in dem sie integriert werden soll (bestimmtes Integral) oder über den gesamten Definitionsbereich (unbestimmtes Integral) stetig ist. Stetig ist eine Funktion, wenn zwischen den Funktionswerten “keine Sprünge” vorhanden sind, d.h. die Funktionswerte des Graphen lassen sich übergangslos (d.h. ohne Sprünge) aneinanderfügen (“man muss beim Zeichnen des Graphens den Stift nicht absetzen”)
Unbestimmte Integrale (die Stammfunktion F(x)) lassen sich je nach Typ der Funktion f(x) mit verschiedenen Rechenoperationen der Integralrechnung lösen. Diese Rechenoperation sind die Differenz-, Potenz- und Faktorregel der Integration. Daneben gibt es noch zwei weitere Operationen für kompliziertere Integrationen, die partielle Integration und die Integration durch Substitution.
Die Integration ist ein grundlegendes Konzept der Mathematik und ein wichtiger Bestandteil der Differential- und Integralrechnung. Sie ermöglicht die Berechnung von Flächen, Volumen oder Zentren von Massen, indem sie eine Funktion mittels einer Integralfunktion zusammenfasst.
Das Symbol für das unbestimmte Integral ist ∫. Es symbolisiert eine Summe von unendlich vielen unendlich kleinen Termini.
Die Grundlegende Integrationsformel ist ∫ f(x) dx = F(x) + C, wobei F(x) die Stammfunktion von f ist und C eine konstante Zahl repräsentiert.
Eine Stammfunktion einer gegebenen Funktion ist eine Funktion, deren Ableitung zu der gegebenen Funktion führt.
Der Hauptsatz der Differential- und Integralrechnung verbindet die Integral- und Differentialrechnung. Es besagt, dass das unbestimmte Integral einer Funktion (die Stammfunktion) und die Ableitung voneinander umgekehrt sind.
Das bestimmte Integral ist ein Integral mit Grenzen. Die Berechnung erfolgt durch die Subtraktion der Werte der Stammfunktion an den Grenzen.
Die Fläche unter einer Funktion wird berechnet, indem man das bestimmte Integral der Funktion über das gegebene Intervall berechnet.
Partielle Integration ist eine Methode zur Berechnung des Integrals von Produkten von Funktionen. Sie ist das Integral-Rechen-Äquivalent zur Produktregel der Differentialrechnung.
Eine Integrierbare Funktion ist eine Funktion, die in einem bestimmten Intervall integriert werden kann, während eine Integralfunktion das Ergebnis dieses Integrationsprozesses ist.
Integration durch Substitution ist eine Methode zur Lösung von Integralen, indem eine kompliziertere Funktion durch eine einfachere ersetzt wird.