Mit Hilfe des Baumdiagramms lassen sich in der Wahrscheinlichkeitsrechnung mögliche Versuchsausgänge von Zufallsexperimenten darstellen und so die Wahrscheinlichkeiten der verschiedenen Versuchsausgänge in einfacher Weise bestimmen.
Allgemein versteht man unter einem Baumdiagramm die graphische Darstellung eines Experiment- bzw. Ereignisverlaufs. Jedes Experiment bzw. Ereignis wird schrittweise dargestellt. Der Vorteil des Baumdiagramms: Es spielt es keine Rolle, ob die Experimente mit oder ohne Wiederholung durchgeführt werden.
Ein Baumdiagramm besteht, ausgehend von einem Startpunkt auf der linken Seite des Blattes bzw. oben, aus einer Anzahl von Ästen, die von diesem Punkt weggehen. Jeder dieser Äste symbolisiert einen möglichen Ausgang des Experimentes (Zahl der verschiedenen Möglichkeiten = Zahl der Äste, z.B. ein Würfelwurf hat 6 mögliche Ergebnisse => 6 Äste gehen vom Startpunkt weg). Von jedem Ende des ersten Experiments (von jedem Ast), geht beim zweiten Experiment erneut eine Anzahl von Ästen aus, die den Ergebnissen dieses Zufallexperimentes entspricht.
Man wirft eine Münze, als mögliches Ereignis gibt es Wappen (w) und Zahl (z). Die Wahrscheinlichkeit für das Eintreten des jeweiligen Ergebnisses ist 0,5 (50%). Da es sich um ein Laplace-Experiment (Ein Laplace-Experiment ist ein Zufallsexperiment bei dem davon ausgegangen wird, dass jeder Versuchsausgang gleich wahrscheinlich ist) handelt, konnte die Wahrscheinlichkeit für jedes Ereignis leicht bestimmt werden. Die Wahrscheinlichkeit des Ergebnisses berechnet sich somit aus: (Anzahl aller Möglichkeiten mit diesem Ergebnis): (Anzahl aller Möglichkeiten) => in diesem Fall: 1 : 2 = 0,5
Nun kann man ein Baumdiagramm für 3 Münzwürfe entwickeln.
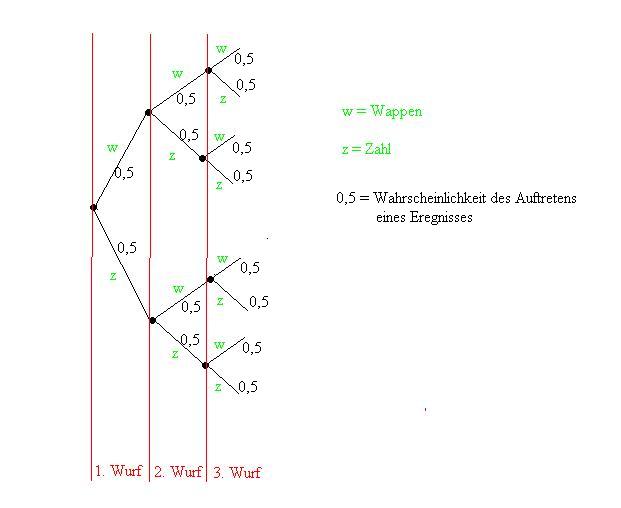
Baumdiagramm für 3 Münzwürfe
Beispiel: Man hätte gerne die Wahrscheinlichkeit, mit der zweimal hintereinander Wappen (w) erscheint und beim dritten Mal die Zahl (z).
Der entsprechende Pfad sieht also so aus: w,w,z Nun multipliziert man die Wahrscheinlichkeiten: 0,5·0,5·0,5 = 0,125 => Die Wahrscheinlichkeit beträgt 12,5%.
Wie in der Einleitung beschrieben, kann das Baumdiagramm-Verfahren auch für Experimente “ohne Zurücklegen” verwendet werden.
Beispiel: Man hat 5 Kugeln, davon 3 schwarze und 3 rote Kugel. Nun zieht man nacheinander eine Kugel.
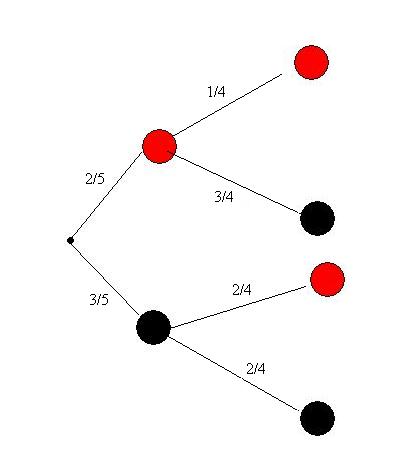
Berechnung der Einzelwahrscheinlichkeiten
Ein Baumdiagramm zur Berechnung von Wahrscheinlichkeiten ist ein visuelles Hilfsmittel, das benutzt wird, um die verschiedenen möglichen Ergebnisse eines Zufallsexperiments darzustellen. Es zeigt alle möglichen Pfade und ihre jeweiligen Wahrscheinlichkeiten.
Man startet von der linken Seite und schreibt das Ereignis auf der rechten Seite, jede Linie stellt einen möglichen Ausgang dar. Die Wahrscheinlichkeit des jeweiligen Ausgangs schreibt man an die entsprechende Linie.
Der Vorteil des Verwendens eines Baumdiagramms in der Wahrscheinlichkeitsrechnung ist, dass es hilft, komplexe Probleme zu strukturieren und vereinfacht die Berechnung von Wahrscheinlichkeiten. Außerdem zeigt es alle möglichen Ergebnisse über einen Blick.
Die Wahrscheinlichkeit eines Ereignisses berechnet man, indem man die Wahrscheinlichkeiten entlang des Pfades zum gewünschten Ereignis multipliziert.
Mehrstufige Zufallsexperimente zeichnet man in einem Baumdiagramm so, dass jede Etappe einen neuen Ast darstellt. Die Wahrscheinlichkeit für jedes Ergebnis ist das Produkt der Wahrscheinlichkeiten ihrer Pfade.
Die Gesamtwahrscheinlichkeit eines Ereignisses berechnet man indem man alle Einzelwahrscheinlichkeiten der Pfade, die zum Ereignis führen, addiert.
Eine bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit, dass ein Ereignis eintritt, unter der Bedingung, dass ein anderes Ereignis bereits eingetreten ist. Sie wird im Baumdiagramm an den entsprechenden Pfaden markiert.
Unabhängige Ereignisse werden in einem Baumdiagramm als Pfade mit gleichen Wahrscheinlichkeiten dargestellt, während abhängige Ereignisse unterschiedliche Wahrscheinlichkeiten haben können.
In einem Baumdiagramm bedeutet das Kreuzen von Pfaden, dass die betreffenden Ereignisse nicht gleichzeitig auftreten können – sie schließen sich gegenseitig aus.
Um die Wahrscheinlichkeit von mehreren unabhängigen Ereignissen in einem Baumdiagramm zu berechnen, multipliziert man einfach die Wahrscheinlichkeiten der jeweiligen Pfade. Wenn die Ereignisse abhängig sind, verwendet man stattdessen die bedingten Wahrscheinlichkeiten.