Eine Einführung in die wichtigen Begriffe: Bedingte Wahrscheinlichkeit

Das Wort “Stochastik” steht für die Gebiete Wahrscheinlichkeitstheorie und Statistik. Beide Teilgebiet sind für fast alle MINT-Fächer von erheblicher Bedeutung. Aus diesem Grund soll auf Lernort-MINT.de in dieses Themengebiet eingeführt werden.

Begriffe in der Wahrscheinlichkeitsrechnung – bedingte Wahrscheinlichkeit

Die bedingte Wahrscheinlichkeit wird definiert als die Wahrscheinlichkeit, dass das Ereignis A eintritt unter der Bedingung, dass auch B eintritt und wird als P(A|B) geschrieben (als “die bedingte Wahrscheinlichkeit von A, vorausgesetzt B” gelesen) , d.h die bedingte Wahrscheinlichkeit verknüpft zwei Ereignisse miteinander. Die bedingte Wahrscheinlichkeit gibt damit für ein Ereignis A die Wahrscheinlichkeit an, dass das Ereignis eintreten wird, vorausgesetzt das Ereignis B ist bereits eingetreten.

Formel: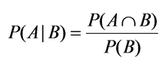 

Was ist der Unterschied?

Die (normale, manchmal auch als totale bezeichnet) Wahrscheinlichkeit ist die Wahrscheinlichkeit für das Eintreten eines Ereignisses A unabhängig von anderen Ereignissen, im Gegensatz dazu ist die bedingte Wahrscheinlichkeit die Wahrscheinlichkeit für das Eintreten eines Ereignisses A unter der Bedingung, dass das Ereignis B eingetreten ist.

Beispiel

In einer Firma gibt es 500 Manager (A) und 1000 Nichtmanager, unterteilt in Personen, die ein Firmenhandy (B) haben und nicht:

Nun kann man sich einige Wahrscheinlichkeiten betrachten:

• Die Wahrscheinlichkeit, jmd. mit Firmenhandy anzutreffen: P(B) = 500 : 1500 = 1/3
• Die Wahrscheinlichkeit, einen Manager anzutreffen: P(A) = 500 : 1000 = 1/3
• Die Wahrscheinlichkeit, einen Manager mit Firmenhandy anzutreffen: Es handelt sich hierbei eine bedingte Wahrscheinlichkeit vor. Es ist die Bedingung, dass es ein Manager (A) ist, also P_A(B) bzw. P (B/A).  P (B/A) = 300 : 500 = 3/5

Eine Einführung in die wichtigen Begriffe: Bedingte Wahrscheinlichkeit – Testfragen/-aufgaben

1. Was ist die Bedeutung von bedingter Wahrscheinlichkeit?

Eine bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit, dass ein Ereignis A stattfindet, gegeben, dass ein anderes Ereignis B eingetreten ist.

2. Wie berechnet man die bedingte Wahrscheinlichkeit?

Die bedingte Wahrscheinlichkeit wird berechnet als das Verhältnis der Wahrscheinlichkeit, dass sowohl Ereignis A als auch Ereignis B eintritt, zur Wahrscheinlichkeit, dass Ereignis B eintritt.

3. Erkläre das Konzept der Unabhängigkeit in Bezug auf die bedingte Wahrscheinlichkeit.

Zwei Ereignisse sind unabhängig, wenn die Eintrittswahrscheinlichkeit eines Ereignisses nicht von der Eintrittswahrscheinlichkeit eines anderen Ereignisses abhängt.

4. Geben Sie ein Beispiel für zwei Ereignisse, die nicht unabhängig sind.

Ein Beispiel für zwei nicht unabhängige Ereignisse könnte sein: Das Ereignis A ist “Es regnet” und das Ereignis B ist “Es gibt eine hohe Luftfeuchtigkeit”. Diese beiden Ereignisse sind nicht unabhängig, da die Wahrscheinlichkeit hoher Luftfeuchtigkeit steigt, wenn es regnet.

5. Wie wirkt sich die bedingte Wahrscheinlichkeit auf die Unabhängigkeit von Ereignissen aus?

Die bedingte Wahrscheinlichkeit kann dazu verwendet werden, zu prüfen, ob zwei Ereignisse unabhängig sind. Wenn die bedingte Wahrscheinlichkeit von A gegeben B gleich der Wahrscheinlichkeit von A ist, dann sind die Ereignisse A und B unabhängig.

6. Was ist der Unterschied zwischen bedingter und unbedingter Wahrscheinlichkeit?

Die unbedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit, dass ein Ereignis eintritt, ohne dass davon ausgegangen wird, dass ein anderes Ereignis eingetreten ist, während die bedingte Wahrscheinlichkeit die Wahrscheinlichkeit ist, dass ein Ereignis eintritt, gegeben, dass ein anderes Ereignis bereits eingetreten ist.

7. Was ist die Formel für bedingte Wahrscheinlichkeit?

Die Formel für die bedingte Wahrscheinlichkeit ist P(A|B) = P(A ∩ B) / P(B). Hier steht P(A|B) für “die Wahrscheinlichkeit von A gegeben B“, P(A ∩ B) steht für “die Wahrscheinlichkeit, dass sowohl A als auch B eintritt“, und P(B) ist die Wahrscheinlichkeit, dass B eintritt.

8. Was bedeutet P(A|B) in der Formel der bedingten Wahrscheinlichkeit?

P(A|B) steht in der Formel der bedingten Wahrscheinlichkeit für “die Wahrscheinlichkeit von A gegeben B“.

9. Was bedeutet P(A ∩ B) in der Formel der bedingten Wahrscheinlichkeit?

P(A ∩ B) steht in der Formel der bedingten Wahrscheinlichkeit für “die Wahrscheinlichkeit, dass sowohl A als auch B eintreten“.

10. Wie berechnet man die Wahrscheinlichkeit eines Ereignisses, wenn man die bedingte Wahrscheinlichkeit und die Wahrscheinlichkeit des bedingenden Ereignisses kennt?

Wenn wir die bedingte Wahrscheinlichkeit P(A|B) und die Wahrscheinlichkeit P(B) kennen, können wir die Wahrscheinlichkeit berechnen, dass sowohl A als auch B eintreten, also P(A ∩ B), durch Multiplikation von P(A|B) mit P(B).