Das Superpositionsprinzip wird gerne in der Mechanik angewandt (aber nicht nur dort, z.B. die Überlagerung von Wellen in der Optik). Dabei erfolgt eine vektorielle Addition von Kräften zu resultierenden Kräften (dies ist auch unter dem Kräfteparallelogramm bekannt). Wichtig ist aber, dass die Größen, die addiert werden, eine Linearität der zugrunde liegenden Gleichungen aufweisen (z.B. Kraft -> F = m·a, linearer Zusammenhang).
Einfach gesagt, ist das Superpositionsprinzip in der Mechanik nichts anders als eine Überlagerung von vektoriellen Größen (d.h. eine Größe, die eine Richtung um einen Betrag hat, wie z.B. Kräfte). Dabei werden die einzelnen Vektoren zu einem resultierenden Vektor addiert.
Wie bereits im allgemeinen Teil erwähnt, befasst sich das Fachgebiet Mechanik mit der Bewegung von Körpern und der Einwirkung von Kräften und stellt z.B. durch die Newtonschen Gesetze den Zusammenhang zwischen Bewegungen einer Masse und den wirkenden Kräften her. In der oben gezeigten Formel für die Kraft (F = m·a) erkennt man, dass eine Linearität der gegeben ist, womit das Superpositionsprinzip angewendet werden kann.
Beispiel zum besseren Verständnis:
Ein Gegenstand wird mit einer Kraft F1 nach oben und mit einer Kraft F2 nach rechts gezogen.
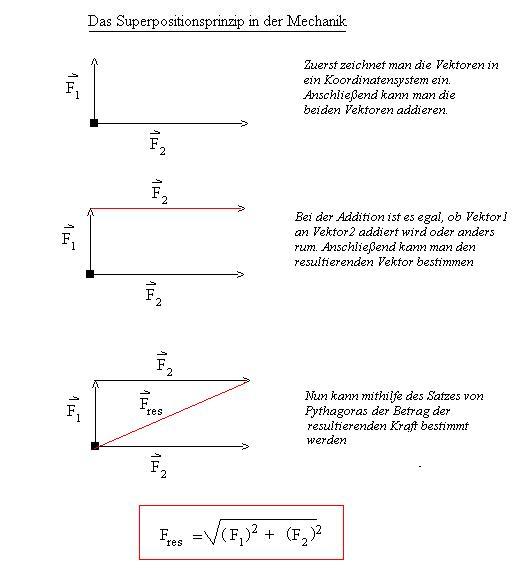
Eine Anwendung des Superpositionsprinzips findet sich z.B. im schrägen Wurf, der sich aus einer gleichförmigen Bewegung und einer gleichförmig, beschleunigten Bewegung zusammensetzt. Dabei versucht man zunächst die einzelnen Bewegungen zu bestimmen und setzt sie dann anschließend additiv zu einer Gesamtbewegung zusammen.
Das Grundprinzip der Superposition in der Mechanik besagt, dass wenn mehrere Kräfte auf einen Körper einwirken, die gesamte Wirkung gleich der vektoriellen Summe der Einzelwirkungen ist.
Das Superpositionsprinzip in der Mechanik findet Anwendung in der Statik, Wellenmechanik und in elastischen Materialien.
Das Superpositionsprinzip ist wichtig, um die Gesamtwirkung von mehreren dynamischen und statischen Einzelfaktoren auf einen mechanischen Körper zu berechnen.
In elastischen Materialien wird das Superpositionsprinzip angewendet, indem die Antwort auf eine ältere Anwendung von Druck oder Kraft nicht von einer neu angelegten Kraft beeinflusst wird.
In der Statik wird das Superpositionsprinzip angewandt, indem einzelne Kräfte aufgebaut und separat betrachtet werden, dann werden die Resultate zusammengefügt, um die Gesamtwirkung zu berechnen.
Eine Bedingung für die Gültigkeit des Superpositionsprinzips in der Mechanik ist, dass das System linear sein muss. Das bedeutet, dass die Antwort des Systems auf einen Eingriff proportional zum Eingriff selbst ist.
Das Superpositionsprinzip ist stark verbunden mit der Linearelastizität, die angibt, dass das Material seine ursprüngliche Form zurückkehrt, sobald die anliegenden Spannungen entfernt sind.
Das Superpositionsprinzip ist manchmal ungenau, weil es auf der Annahme beruht, dass das System linear ist. In der Realität können jedoch nichtlineare Effekte auftreten.
Das Superpositionsprinzip kann mit der Vektoraddition erklärt werden, da es die Anwendung von mehreren Kräften auf einen Körper betrachtet und die gesamte Kraftwirkung als die vektorielle Summe dieser Kräfte betrachtet.
Das Superpositionsprinzip ist mit dem Gesetz von Hooke verknüpft, da dieses Gesetz ebenfalls ein lineares Verhalten von Materialien unter Spannung beschreibt und damit die Basis des Superpositionsprinzips in der Mechanik bildet.