Schräger Wurf

Nachdem in den vorangegangenen Kapiteln die Grundlagen der Mechanik erläutert wurden, soll nun auf Anwendungen eingegangen werden. Eine interessante Anwendung ist der schräge Wurf, bei dem ein Körper unter einem Winkel relativ zum Horizont abgeworfen wird. Der schräge Wurf ist eine Kombination (Superpositionsprinzip, d.h. Teilbewegungen überlagern sich zu einer resultierenden Gesamtbewegung) aus gleichförmiger Bewegung (in x-Richtung) in Abwurfrichtung und freiem Fall (in y-Richtung).

Der schräge Wurf

Wie bereits in der Einleitung erwähnt, ist der schräge Wurf eine Kombination aus einer gleichförmigen Bewegung und einer gleichmäßig beschleunigten Bewegung (freier Fall).

Herleitung der sog. “Bahngleichung”

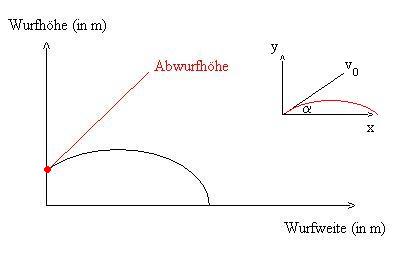
Für die Herleitung werden die Formel für die gleichförmige Bewegung (x-Richtung) und gleichmäßig beschleunigte Bewegung (in y-Richtung) verwendet. Bei der Herleitung der Formeln darf man aber nicht vergessen, dass man ein v₀ in x-Richtung und ein v₀ in y-Richtung hat, dabei gilt: v₀ (in x-Richtung) = v₀· cos(a) und v₀ (in y-Richtung) = v₀·sin(a) .
Herleiten lässt sich dies unter Anwendung der Trigonometrie: (Cosinus = Ankathete durch Hypotenuse und Sinus = Gegenkathete durch Hypotenuse, Hypotenuse ist hierbei im Diagramm v₀)

Dies kann man nun einsetzen:

• Die Formel für die gleichförmige Bewegung lautet: s = v·t  => x =  v₀ · cosa ·t
• Die Formel für die gleichmäßig beschleunigte Bewegung lautet: s = s₀ + 0,5·a·t² + v·t => y = h₀ + 0,5·g·t² + v₀·sina ·t

aus diesen Formeln kann man alle gewünschten physikalischen Größen wie max. Wurfhöhe (= max. y-Wert), max. Steigzeit und max. Wurfweite (= max. x-Wert) bestimmen. Für die Bestimmung der Bahnkurve des schrägen Wurfes müssen -wie bereits erwähnt- die Komponente in x-Richtung und in y-Richtung kombiniert werden. Dabei wird Gleichung für die x-Richtung nach der Zeit t aufgelöst  (t = x : (v₀·cos a ) und das Ergebnis für “t” in die Gleichung für die y-Richtung eingesetzt:

Formeln beim schrägen Wurf:

• gleichförmige Bewegung

• gleichmäßig beschleunigte Bewegung

Schräger Wurf – Testfragen/-aufgaben

1. Was versteht man unter dem Begriff “schräger Wurf” in der Physik?

Der schräge Wurf ist eine Bewegung, bei der ein Körper sowohl in horizontaler als auch in vertikaler Richtung bewegt wird. Diese Bewegung ergibt eine Parabel.

2. Welche beiden Bewegungen werden beim schrägen Wurf kombiniert?

Beim schrägen Wurf werden die gleichförmige Bewegung und die gleichmäßig beschleunigte Bewegung kombiniert.

3. Wie verhält sich die horizontale Geschwindigkeit beim schrägen Wurf?

Die horizontale Geschwindigkeit beim schrägen Wurf bleibt konstant, da keine horizontalen Kräfte wirken (Vernachlässigung der Luftwiderstands).

4. Wie verhält sich die vertikale Geschwindigkeit beim schrägen Wurf?

Die vertikale Geschwindigkeit beim schrägen Wurf ändert sich aufgrund der Erdanziehung.

5. Wie berechnet man die Wurfweite beim schrägen Wurf?

Die Wurfweite beim schrägen Wurf errechnet man mit der Formel Wurfweite = (v²/g) * sin(2*α), wobei v die Abwurfgeschwindigkeit, g die Gravitationskonstante und α der Abwurfwinkel ist.

6. Was beschreibt die Flugkurve beim schrägen Wurf?

Die Flugkurve beim schrägen Wurf beschreibt eine Parabel.

7. Was passiert, wenn der Abwurfwinkel beim schrägen Wurf 45 Grad beträgt?

Wenn der Abwurfwinkel bei einem schrägen Wurf 45 Grad beträgt, wird die größtmögliche Wurfweite erzielt.

8. Wie berechnet man die maximale Höhe beim schrägen Wurf?

Die maximale Höhe beim schrägen Wurf kann mit der Formel Hmax = (v² * sin²(α)) / 2g berechnet werden.

9. Wie lässt sich die Flugzeit beim schrägen Wurf berechnen?

Die Flugzeit beim schrägen Wurf lässt sich mit der Formel Flugzeit = 2*v*sin(α) / g berechnen.

10. Was wäre anders, wenn beim schrägen Wurf der Luftwiderstand berücksichtigt wird?

Wird beim schrägen Wurf der Luftwiderstand berücksichtigt, ist die Flugkurve keine exakte Parabel mehr und die horizontale Geschwindigkeit bleibt nicht konstant, sondern nimmt ab.