Berechnungen im Dreieck – Rechtwinklige und schiefwinklige Dreiecke

Bei einem Dreieck handelt es sich um eine geometrische Figur mit drei Seiten und drei Ecken aufweist. Die Eckpunkte eines Dreiecks werden immer in Großbuchstaben und gegen den Uhrzeigersinn klassifiziert, die Seiten des Dreiecks immer Kleinbuchstaben und gegenüber der Eckpunkte. Dreiecke werden dabei entweder durch die Winkel oder die Seitenlänge klassifiziert.

Einteilung Winkelgröße:

• Sind alle Winkel kleiner als 90°, so handelt es sich um ein spitzwinkliges Dreieck.
• Beträgt ein Winkel 90°, so handelt es sich um ein rechtwinkliges Dreieck.
• Ist ein Winkel größer als 90°, so handelt es sich um ein stumpfes Dreieck

In der Schulmathematik vereinfacht sich die Einteilung von Dreiecken (anhand des Winkels) indem man spitzwinklige und stumpfe Dreiecke zu einer Dreieckklasse zusammenführt: schiefwinklige Dreiecke. Daher unterscheiden wir nur noch das rechtwinklige Dreieck und das schiefwinklige Dreieck.

Im Rahmen dieses Kapitels werden nun die Formeln für Berechnungen in einem rechtwinkligen und einem schiefwinkligen Dreieck vorgestellt:

Berechnungen im rechtwinkligen und schiefwinkligen Dreieck

Nachfolgend sind die beiden Dreieck-Arten abgebildet: das schiefwinklige und das rechtwinklige Dreieck:

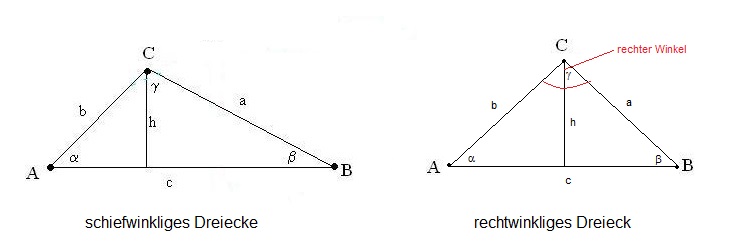
Berechnungen im rechtwinkligen und schiefwinkligen Dreieck

Formeln in einem rechtwinkligen Dreieck:

Wie im Kapitel “Satz des Pythagoras” vorgestellt, gilt in einem rechtwinkligen Dreieck der Satz des Pythagoras. Nach dem Satz des Pythagoras gilt, dass die Summe der Quadrate der Katheten a und b gleich dem Quadrat der Hypotenuse c ist:

a² + b² = c²

Da in einem rechtwinkligen Dreieck alle Seiten definiert sind (die Seite, die dem rechten Winkel gegenüber liegt, wird als Hypotenuse bezeichnet, die beiden anderen Seiten, die den rechten Winkel bilden, werden als Katheten bezeichnet) kann man die Seitenlängen und die Winkel zueinander in Bezug setzen. Dies wird u.a. bei der Berechnung von Winkelgrößen benötigt:

• sin α = a : c
• cos α  = b : c
• tan α = a : b

Da nun zwei Winkel bekannt sind, kann man den dritten Winkel auch ausrechnen.

Formeln in einem schiefwinkligen Dreieck

Die Herleitung der entsprechenden Formeln in einem schiefwinkligen Dreieck ist auch nicht viel schwieriger, hier macht man sich zunutze, dass durch die Höhe h das schiefwinklige Dreieck geteilt wird. Durch die Teilung entstehen dabei wieder zwei rechtwinklige Dreiecke, in denen der Satz des Pythagoras gilt:

• sin α = h : b
• sin β = h : a
• =>  b sin α = a sin β

Hieraus leitet sich der Sinus-Satz (für Berechnungen im schiefwinkligen Dreieck) ab:

a : sin α = b : sin β = c : sin γ

Der Sinus-Satz lässt sich “sinngemäß” wiedergeben mit:

• Die Seiten a, b, c in einem schiefwinkligen Dreieck verhalten sich wie der “Sinus” der den Seiten gegenüberliegenden Winkel.
• Wenn man die Formel etwas umwandelt, gilt auch, dass das Verhältnis zweier Dreiecksseiten gleich dem Verhältnis des Sinus der gegenüberliegenden Winkel ist:  a : b = sin α : sin β

In einem schiefwinkligen Rechteck gilt auch der Cosinus-Satz.

Ohne weitere Herleitungen (siehe dazu das entsprechende Kapitel) der Cosius-Satz bzw. Sätze

a² = b² + c² – 2·b·c·cos α
b² = a² + c² – 2·a·c·cos β
c² = a² + b² – 2·a·b·cos γ

Sinngemäß sagt der Cosinus-Satz aus, dass das Quadrat einer Dreiecksseite in einem schiefwinkligen Dreieck gleich der Summe der Quadrate der beiden anderen Seiten ist minus zweimal dem Produkt aus diesen beiden Seiten und dem Cosinus des Zwischenwinkels beider Seiten.

Berechnungen im Dreieck – Rechtwinklige und schiefwinklige Dreiecke – Testfragen/-aufgaben

1. Definieren Sie ein rechtwinkliges Dreieck.

Ein rechtwinkliges Dreieck ist ein Dreieck, in dem eine Ecke einen rechten Winkel (90 Grad) hat.

2. Was ist das Pythagoreische Theorem und wie wird es in rechtwinkligen Dreiecken angewendet?

Das Pythagoreische Theorem besagt, dass in einem rechtwinkligen Dreieck das Quadrat der Länge der Hypotenuse (der Seite gegenüber dem rechten Winkel) gleich der Summe der Quadrate der Längen der beiden anderen Seiten ist.

3. Definieren Sie ein schiefwinkliges Dreieck.

Ein schiefwinkliges Dreieck ist ein Dreieck, das keinen rechten Winkel hat. Alle Winkel sind kleiner als 90 Grad.

4. Was ist der Sinussatz und wie wird er in schiefwinkligen Dreiecken angewendet?

Der Sinussatz ist eine Beziehung zwischen den Längen der Seiten eines Dreiecks und den Sinuswerten seiner Winkel. In jedem Dreieck ist das Verhältnis der Länge einer Seite zum Sinus des gegenüberliegenden Winkels für alle drei Seiten gleich.

5. Was ist der Kosinussatz und wie wird er in schiefwinkligen Dreiecken angewendet?

Der Kosinussatz bezieht die Längen der Seiten eines Dreiecks auf den Kosinus eines seiner Winkel. Es wird verwendet, wenn über zwei Seiten und dem eingeschlossenen Winkel Information vorliegt.

6. Wie berechnet man die Fläche eines rechtwinkligen Dreiecks?

Die Fläche eines rechtwinkligen Dreiecks wird berechnet, indem man die Längen der zwei Seiten, die den rechten Winkel bilden, multipliziert und dann durch zwei teilt.

7. Wie berechnet man die Fläche eines schiefwinkligen Dreiecks?

Die Fläche eines schiefwinkligen Dreiecks kann mit Hilfe der Seitenlängen und des Sinus des eingeschlossenen Winkels berechnet werden, mittels der Formel: 1/2abSin(C).

8. Was ist die Bedeutung der Tangensfunktion in einem rechtwinkligen Dreieck?

Im rechtwinkligen Dreieck ist der Tangens eines Winkels das Verhältnis der Länge der gegenüberliegenden Seite zur angrenzenden Seite.

9. Was ist der Unterschied zwischen einem spitzen und einem stumpfen Winkel?

Ein spitzer Winkel ist kleiner als 90 Grad, während ein stumpfer Winkel größer als 90 Grad aber kleiner als 180 Grad ist.

10. Wie kann man die Längen der Seiten in einem schiefwinkligen Dreieck berechnen?

Die Längen der Seiten eines schiefwinkligen Dreiecks können unter Verwendung des Sinussatzes oder des Kosinussatzes berechnet werden, abhängig von den gegebenen Informationen.