Volumen eines Zylinders

Das Volumen eines Zylinders zu bestimmen ist nicht nur eine Aufgabe in der Mathematik (=> Geometrie), sondern auch aus anderen naturwissen- schaftlichen Fächern. Dies kann beispielsweise das Fach Chemie sein, in dem man das Volumen eines (ungraduierten) Glaszylinders bestimmen will, der mit Flüssigkeit gefüllt wird.

Auch wenn sich der geometrische Körper “Zylinder” aus zwei Kreisflächen und einer Mantelfläche zusammensetzt, so ist dennoch die Formel zur Bestimmung des Volumens eines Zylinders relativ einfach: Das Volumen = Grundfläche • Höhe des Zylinders

Volumen eines Zylinders

Wie eingangs erwähnt, ist das Volumen eines Zylinder = Grundfläche • Höhe

Ein Zylinder besteht dabei aus zwei Kreisflächen und einer Mantelfläche. Der geometrische Körper entsteht dadurch, das man bei zwei gleichgroßen Kreisen (die genau übereinanderliegen) die gegenüberliegenden Kreisränder miteinander verbindet (siehe dazu nachfolgende Abbildung)

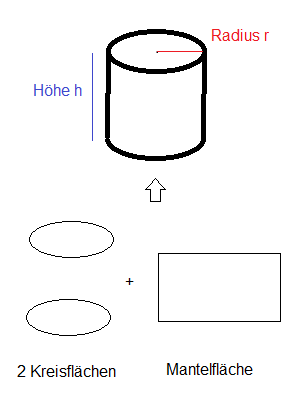
Volumen eines Zylinders

Wie in der Abbildung ersichtlich ist die Grundfläche eines Zylinders immer ein Kreis. Daher wird bei der Volumenberechnung eines Zylinders als Grundfläche immer die Kreisfläche verwendet. Das Volumen eines Zylinders ist also das Produkt aus Kreisfläche und Höhe. Die Formel zur Berechnung eines Zylindervolumens lautet:

V = π · r² · h

Weitere Formeln in Zusammenhang eines Zylinders:

• Grundfläche eins Zylinders = π · r²
• Mantelfläche eines Zylinders = Umfang · Höhe = 2 · π · r · h
• Oberfläche eines Zylinders = 2 · Grundfläche + Mantelfläche = 2 · π · r² + 2 · π · r · h = 2 · π · r² · (r + h)

Volumen eines Zylinders – Testfragen/-aufgaben

1. Was ist die allgemeine Formel zur Berechnung des Volumens eines Zylinders?

Die allgemeine Formel zur Berechnung des Volumens eines Zylinders ist V = πr²h, wobei V das Volumen, π die mathematische Konstante pi (~3.14159), r der Radius des Zylinders und h die Höhe des Zylinders ist.

2. Was ist der Radius eines Zylinders?

Der Radius eines Zylinders ist die Entfernung vom Mittelpunkt der Basis (ein Kreis) bis zu seinem Rand.

3. Was ist die Höhe eines Zylinders?

Die Höhe eines Zylinders ist der Abstand zwischen den zwei Basen (die Kreise).

4. Welche Einheit wird in der Regel verwendet, um das Volumen eines Zylinders zu messen?

Das Volumen eines Zylinders wird in der Regel in Kubikeinheiten gemessen, wie zum Beispiel Kubikmeter oder Kubikzentimeter.

5. Wie ändert sich das Volumen eines Zylinders, wenn der Radius verdoppelt wird?

Wenn der Radius eines Zylinders verdoppelt wird, wird das Volumen des Zylinders vervierfacht (weil das Quadrat des verdoppelten Radius 4-mal größer ist).

6. Wie ändert sich das Volumen eines Zylinders, wenn die Höhe verdoppelt wird?

Wenn die Höhe eines Zylinders verdoppelt wird, dann wird auch das Volumen des Zylinders verdoppelt.

7. Wie berechnet man das Volumen eines Zylinders, wenn der Durchmesser anstelle des Radius gegeben ist?

Wenn der Durchmesser anstelle des Radius gegeben ist, halbiert man diesen, um den Radius zu erhalten. Man verwendet dann den Radius in der Formel zur Berechnung des Volumens.

8. Was passiert mit dem Volumen eines Zylinders, wenn sowohl der Radius als auch die Höhe verdoppelt werden?

Wenn sowohl der Radius als auch die Höhe eines Zylinders verdoppelt werden, wird das Volumen des Zylinders achtmal größer (zweimal das Vierfache).

9. Wie ändert sich das Volumen eines Zylinders, wenn der Radius halbiert wird?

Wenn der Radius eines Zylinders halbiert wird, wird das Volumen des Zylinders ein Viertel so groß.

10. Wie ändert sich das Volumen eines Zylinders, wenn die Höhe halbiert wird?

Wenn die Höhe eines Zylinders halbiert wird, wird auch das Volumen des Zylinders halbiert.