Trigonometrische Funktionen

Das Themengebiet “Rechnen im Dreieck” ist eine der wichtigsten Werkzeuge bzw. Hilfsmittel der analytischen Geometrie und kommt nicht nur in der Mathematik zum Einsatz. In den nachfolgenden Kapiteln soll jeweils kurz auf die wichtigsten Eigenschaften in einem Dreieck eingegangen werden.

In diesem Teil sollen die trigonometrischen Funktionen bei Dreiecken näher untersucht werden.

Trigonometrische Funktionen bei Dreiecken

Trigonometrische Funktionen werden auch manchmal als Winkelfunktionen bezeichnet, da sie bei geometrischen Figuren einen Zusammenhang zwischen einem Winkel und Seitenverhältnissen der Figur wiedergeben. Diese Funktionen (wie z.B. die Sinusfunktion, Kosinusfunktion und Tangensfunktion) sind Grundwerkzeuge im Bereich der analytischen Geometrie. Nachfolgend sind die wichtigsten Funktionen dargestellt:

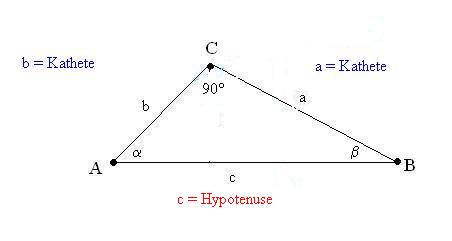
Trigonometrische Funktionen bei Dreiecken

Die Anwendung der trigonometrischen Funktionen bei Dreiecken setzt voraus, dass es sich um ein rechtwinkliges Dreieck handelt. Dabei stehen in einem rechtwinkligen Dreieck die Seitenverhältnisse in Beziehung zu den Winkeln. Die Seiten werden dabei in die Hypotenuse und die Katheten unterschieden, wobei die Katheten nochmals in Ankathete und Gegenkathete unterschieden werden.

• Hypotenuse: Die Hypotenuse (in einem rechtwinkligen Dreieck) ist die Seite, die dem rechten Winkel (90°) gegenüber liegt (in unserem Beispiel also die Seite c). Damit ist sie auch die längste Seite im rechtwinkligen Dreieck.
• Die anderen beiden Seiten im Dreieck werden als Katheten bezeichnet. Zur Unterscheidung, ob An- oder Gegenkathete muss man einen bestimmten Winkel betrachten. Die Ankathete ist dabei die Kathete, die an dem Winkel anliegt, die Gegenkathete ist die Kathete, die dem Winkel gegenüberliegt (z.B. Betrachten wir den Winkel “alpha”, so ist die Seite c die Hypotenuse (da wird nicht weiter unterschieden), die Seite (Kathete) b liegt am Winkel alpha an und ist deshalb die Ankathete und somit die Seite a die Gegenkathete.

Trigonometrische Funktionen:

• sin (Winkel) = Gegenkathete : Hypotenuse
• cos (Winkel) = Ankathete : Hypotenuse
• tan (Winkel) = Gegenkathete : Ankathete
• cot (Winkel) = Ankathete : Gegenkathete

Beispiel:

Gesucht ist z.B. der tan (ß(beta)) = Gegenkathete : Ankathete. In dem jetzigen Fall nehmen wir dem Winkel “beta” als Betrachtungspunkt, damit ist die Ankathete (die Kathete, die an “beta” anliegt) die Seite a und damit die Seite b die Gegenkathete.

Damit ist die Lösung von tan (ß(beta)) = Gegenkathete : Ankathete = b : a

Anmerkung:

Im Kapitel “Allgemeines über Dreiecke” wurde auch die Notation bei Dreiecken vorgestellt. Die Nummerierung der Ecken (mit Großbuchstaben) erfolgt gegen den Uhrzeigersinn, die gegenüberliegenden Seiten erhalten den entsprechenden Kleinbuchstaben. Nun könnte man damit sagen, dass es logisch ist, dass die Seite a, die der Ecke A (und damit dem Winkel “alpha”) gegenüberliegt, die Gegenkathete (wenn man den Winkel “alpha” betrachtet) sein muss. Normalerweise ist das auch richtig, in Prüfungen kann man aber auch anders nummerieren, deswegen sollt man nie bestimmen, was Ankathete und Gegenkathete ist, ohne das Dreieck gesehen zu haben.

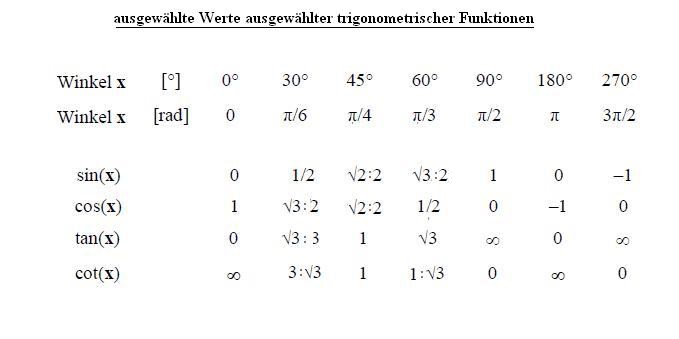
Ausgewählte Funktionswerte bei trigonometrischen Funktionen

Ausgewählte Funktionswerte bei trigonometrischen Funktionen

Trigonometrische Funktionen – Testfragen/-aufgaben

1. Was ist eine Trigonometrische Funktion?

Eine Trigonometrische Funktion ist eine mathematische Funktion, die das Verhältnis zwischen den Seitenlängen eines rechten Winkels in einem Dreieck angibt.

2. Wie berechnet man den Sinus eines Winkels?

Der Sinus eines Winkels berechnet sich als die Länge der Gegenkathete geteilt durch die Länge der Hypotenuse in einem rechtwinkligen Dreieck.

3. Wie berechnet man den Cosinus eines Winkels?

Der Cosinus eines Winkels berechnet sich als die Länge der Ankathete geteilt durch die Länge der Hypotenuse in einem rechtwinkligen Dreieck.

4. Wie berechnet man den Tangens eines Winkels?

Der Tangens eines Winkels berechnet sich als das Verhältnis der Länge der Gegenkathete zur Länge der Ankathete in einem rechtwinkligen Dreieck.

5. Wie lautet die Definition vom Sinus-Cosinus-Theorem?

Das Sinus-Cosinus-Theorem besagt, dass sich das Verhältnis der Seitenlängen in jedem Dreieck als Funktion der Winkel ausdrücken lässt.

6. Was ist ein Einheitskreis?

Ein Einheitskreis ist ein Kreis mit dem Radius 1, der oft zur Veranschaulichung von Trigonometrischen Funktionen benutzt wird.

7. Wie hängen Sinus und Cosinus zusammen?

Es gilt sin²(x) + cos²(x) = 1. Daraus folgt, dass der Sinus und der Cosinus eines Winkels sich immer zu 1 ergänzen.

8. Was sind die Perioden von Sinus und Cosinus?

Die Perioden von Sinus und Cosinus sind jeweils 2π (oder 360 Grad), da ihre Werte sich alle 2π bzw. alle 360 Grad wiederholen.

9. Was passiert, wenn man den Sinus und den Cosinus eines Winkels addiert?

Wenn man den Sinus und den Cosinus eines Winkels addiert, erhält man nicht unbedingt 1, da die Winkel, auf die sie sich beziehen, unterschiedlich sind.

10. Was bedeutet “Reziproke Trigonometrische Funktionen”?

Reziproke Trigonometrische Funktionen sind Funktionen, die durch das Umkehren der gewöhnlichen Trigonometrischen Funktionen entstehen. Dazu zählen Cosecans, Secans und Cotangens.