Die pq-Formel zur Lösung einer quadratischen Gleichung

Was ist eine quadratische Gleichung?

Eine quadratische Gleichung ist eine Gleichung, die sich in der Form x² + px + q = 0 schreiben lässt. Um diese Gleichung zu Lösen gibt es eine Lösungsformel, die auch als pq-Formel bekannt ist. Mit Hilfe der pq-Formel kann man eine quadratische Gleichung lösen, die in allgemeiner Form gegeben ist.

Die pq-Formel

Wie eingangs erwähnt, wird die pq-Formel immer dann verwendet, wenn eine quadratische Gleichung der Form x² + px + q = 0  vorliegt. Die pq-Formel zur Lösung einer solchen quadratischen Gleichung lautet:

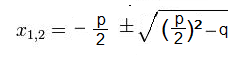
Der erste Schritt zur Lösung einer quadratischen Gleichung mit Hilfe der pq-Formel ist immer, die Gleichung in die Form x² + px + q = 0 zu überführen. Anschließend werden die Variablen “p” und “q” bestimmt und in die pq-Formel eingesetzt.

Hinweise zum Umgang mit der pq-Formel:

• In der Regel gelten in der Schule die Menge der reellen Zahlen, daher kann unter der Wurzel der pq-Formel keine negative Zahl stehen. Sollte dennoch ein negativer Wert unter der Wurzel stehen, da hat die pq-Formel kein Ergebnis. Dies bedeutet, dass die quadratische Gleichung keine Lösung hat (was auch durchaus vorkommen kann).
• Die pq-Formel zeigt, dass es für Gleichungen der Form x² + px + q = 0  nur maximal zwei Lösungen gibt.
• Liegt eine Gleichung nicht in der Form x² + px + q = 0 vor, so muss sie in diese umgewandelt werden. Die passende Form für die pq-Formel erhält man, indem man die Gleichung durch den Koeffizienten vor dem x² teilt.
• Die Herleitung der pq-Formel erfolgt über die quadratische Ergänzung und die binomischen Formeln. x² + px + q = 0 => x² + px + (p/2)² – (p/2)² +q = 0 => x² + px + (p/2)² = (p/2)² – q  => (x + [p/2])² = (p/2)² – q  => Wurzel ziehen und [p/2] von der linken auf die rechte Seite bringen.

Die pq-Formel zur Lösung einer quadratischen Gleichung – Testfragen/-aufgaben

1. Was ist das Hauptziel der Verwendung der pq-Formel?

Das Hauptziel der Verwendung der pq-Formel ist die Lösung einer quadratischen Gleichung der Form x²+px+q=0.

2. Wie lautet die pq-Formel?

Die pq-Formel lautet x₁/₂=-p/2±√((p/2)²-q).

3. Welche Werte repräsentieren p und q in der Gleichung?

In der Gleichung repräsentieren p und q jeweils Koeffizienten: p ist der Koeffizient des x-Terms und q ist der konstante Term.

4. Was repräsentiert der Diskriminant in der pq-Formel?

Der Diskriminant, (p/2)²-q, in der pq-Formel bestimmt die Anzahl und Art der Lösungen der quadratischen Gleichung.

5. Was passiert, wenn der Diskriminant größer als Null ist?

Wenn der Diskriminant größer als Null ist, gibt es zwei verschiedene reale Lösungen für die quadratische Gleichung.

6. Was passiert, wenn der Diskriminant gleich Null ist?

Wenn der Diskriminant gleich Null ist, gibt es eine reale Lösung (oder zwei identische reale Lösungen) für die quadratische Gleichung.

7. Was passiert, wenn der Diskriminant kleiner als Null ist?

Wenn der Diskriminant kleiner als Null ist, gibt es keine reale Lösung, sondern zwei komplexe Lösungen für die quadratische Gleichung.

8. Wie kann die pq-Formel zur Lösung von Anwendungsproblemen verwendet werden?

Die pq-Formel kann in Anwendungsproblemen zur Lösung von Problemen verwendet werden, in denen eine quadratische Funktion modelliert wird, z.B. in der Physik, Wirtschaft, Ingenieurwissenschaften etc.

9. Wie kann man die pq-Formel umformen, wenn die quadratische Gleichung nicht in Normalform ist?

Wenn die quadratische Gleichung nicht in Normalform ist, kann man sie durch Division durch den Koeffizienten von x² in die Form x²+px+q=0 bringen und anschließend die pq-Formel anwenden.

10. Welche Art von Gleichungen kann man nicht mit der pq-Formel lösen?

Die pq-Formel kann keine linearen oder kubischen Gleichungen lösen, sie ist spezifisch für quadratische Gleichungen der Form x²+px+q=0.