Auch in natur- und ingenieurwissenschaftlicher Vorgängen ist es grundsätzlich nicht möglich, fehlerfrei zu messen. Die Abweichungen der Messwerte von den wahren Werten wirken sich auf ein Messergebnis aus, so dass dieses ebenfalls von seinem wahren Wert abweicht und einiges über den Messvorgang ausgesagt werden kann, beispielsweise ob systematische (z.B. fehlerhaftes Messgerät) oder zufällige Fehler vorliegen. Im folgenden werden einige Möglichkeiten zur Fehlerangabe beschrieben:
Die einfachste Art mit unterschiedlichen Einzelergebnissen fertig zu werden, ist, ihren Mittelwert, also z.B. den Mittelwert der Eigenschaften von Molekülen, zu betrachten. Der Mittelwert einer Stichprobe x, …, xi ist definiert als das arithmetische Mittel der Stichprobenwerte. Weiterhin ist i die Anzahl der Stichproben:
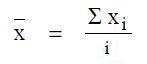 oder
oder Dieser Mittelwert allein ist aber häufig nicht brauchbar. Man benötigt also eine weitere Größe, die Streuung der Einzelwerte:
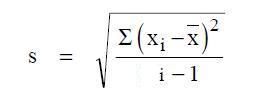
Die Abweichungen der (Mess)Werte vieler natur- und ingenieurwissenschaftlicher Vorgänge vom Mittelwert lassen sich durch die Normalverteilung entweder exakt oder wenigstens in sehr guter Näherung durch die Normal- oder Gauß-Verteilung beschrieben.
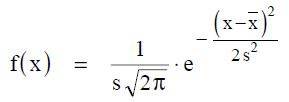
Beim Rechnen mit naturwissenschaftlichen Größen gelten Grundregeln für die Ergebnisse:
Der Mittelwert ist der Durchschnittswert einer Datenmenge. Er wird berechnet, indem man die Summe aller Werte durch die Anzahl der Werte teilt.
Die Streuung gibt Aufschluss über die Verteilung der Werte. Ein hoher Streuwert bedeutet, dass die Werte stark voneinander abweichen; ein geringer Streuwert zeigt, dass die Werte eng beieinander liegen.
Eine normalverteilte Datenmenge hat die Form einer Glockenkurve, bei der die meisten Werte um den Mittelwert herum liegen. Die Verteilung fällt zu den beiden Enden hin ab.
Der Median ist der Wert, der genau in der Mitte einer geordneten Datenreihe liegt. Es gibt also genau so viele Werte, die größer als der Median sind, wie Werte, die kleiner sind.
Der Mittelwert ist durch extrem hohe oder niedrige Werte beeinflussbar, der Median hingegen nicht. Deshalb ist der Median ein robusteres Maß als der Mittelwert, wenn es um die zentrale Tendenz geht.
Der Modus ist der Wert, der in einer Verteilung am häufigsten vorkommt.
Die Varianz ist ein Maß für die Streuung der Datenpunkte um ihren Mittelwert. Sie zeigt, wie stark die Werte voneinander abweichen.
Die Standardabweichung ist die Quadratwurzel aus der Varianz und gibt ebenfalls die Streuung der Datenpunkte um den Mittelwert an.
Eine bivariate Verteilung ist eine Art der Verteilung, bei der zwei Variablen gleichzeitig betrachtet werden. Sie zeigt also den Zusammenhang zwischen zwei Variablen.
Ein Histogramm ist eine graphische Darstellung der Häufigkeitsverteilung in einem Datensatz. Es zeigt, wie oft bestimmte Werte oder Wertebereiche in der Datenmenge vorkommen.