Wie jede Bewegung folgt auch die Bewegung der Erde (die um die Sonne kreist) physikalischen Gesetzen. Diese zugehörigen (drei) physikalischen Gesetze wurden vom Johannes Kepler formuliert.Dabei beschäftigt sich das 3. Keplersche Gesetz mit Umlaufszeiten und Sonnenentfernung von Planeten in unserem Sonnensystem. Das 3. Keplersche Gesetz besagt, dass die Quadrate der Umlaufzeiten der Planeten um die Sonne sich so verhalten wie die dritten Potenzen der mittleren Entfernungen der Planeten von der Sonne.
Wie bereits eingangs erwähnt, gibt das 3. Keplersche Gesetz den Zusammenhang zwischen der Größe der Kreisbahn eines Planeten und der Zeit für eine Umkreisung der Sonne wieder. Die Quadrate der Umlaufzeiten der Planeten um die Sonne verhalten sich so wie die dritten Potenzen der mittleren Entfernungen der Planeten von der Sonne:
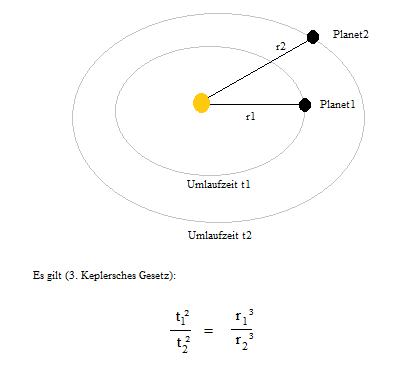
Das 3. Keplersche Gesetze dient also dazu, die (relativen) Umlaufzeiten der Planeten und die Entfernung zur Sonne zu bestimmen. Mit Hilfe dieses Gesetzes kann also die Größe unseres Planetensystems (Entfernung Sonne-Planet) bestimmt werden.
Wie erwähnt, kann mit dem 3. Keplerschen Gesetz eine relative Entfernung bestimmt werden. Es ist nicht möglich, eine direkte Entfernung zu bestimmen. Das 3. Keplersche Gesetz heißt nicht, dass das Quadrat der Umlaufzeit der 3. Potenz der mittleren Entfernung eines Planeten zur Sonne entspricht (siehe Aufgaben weiter unten).
Beweis des 3. Keplerschen Gesetzes:
Für Planetenbewegung gelten die allgemeinen physikalischen Gesetze, so dass wir zum Beweis der Richtigkeit des 3. Keplerschen Gesetzes die
grundlegenden Newtonschen Gesetzen der Mechanik verwenden. Wie bereits beim Beweis der Gültigkeit des 2. Keplerschen Gesetzes basiert unser Beweis auf der Grundlage, dass ein Planet auf einer Kreisbahn um die Sonne kreist. Damit der Planet sich auf einer stabilen Kreisbahn bewegt, halten sich die Gravitationskraft und Zentripetalkraft im Gleichgewicht (beide Kräfte sind also betragsmäßig gleich).
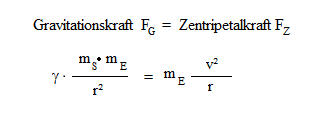
Wie wir in unserem physikalischen Ansatz sehen, können wir die Masse der Erde auf beiden Seiten kürzen. Die Masse der Erde (oder eines anderen Planten) spielt daher keine Rolle.
Setzen wir die Formel für die Bahngeschwinigkeit ein
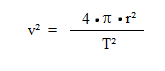
Erhalten wir damit folgende Gleichung
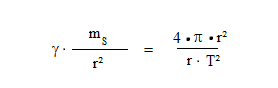
Nun formulieren wir die Gleichung etwas um

Allgemein: Der Quotient aus (zweiter Potenz der Umlaufdauer eines Planeten) und (dritter Potenz der mittleren Entfernung Planet Erde) ist konstant
Hinweis: Wir haben die Gültigkeit des 3. Keplerschen Gesetzes bewiesen, indem wir die Gravitationskraft und die Zentripetalkraft gleichgesetzt haben.
Dafür haben wir folgende “Fakten” angenommen:
Aufgabe zur Anwendung des 3. Keplerschen Gesetzes:
Wir wollen nun ermitteln, wie lange der Mars benötigt, um die Sonne zu umkreisen.
Der mittlere Abstand von Mars und Sonne beträgt 1,52 AE (AE = astronomische Einheit, Info: der mittlere Abstand zwischen Erde und Sonne beträgt 1 AE)
Ansatz : TM2 : TE2 = rM3 : rE3 = 1,523 : 13 = 1,523
Lösung: TM2 = 1,523 · TE2 (TE = 1 Jahr)
Ergebnis: TM = 1,88 TE = 1,88 Jahre
Sehen wir nun in einem Lexikon nach, z.B. Wikipedia (https://de.wikipedia.org/wiki/Mars_(Planet)#Umlaufbahn), so wird dort eine Umlaufzeit von 687 Tagen angegeben, was ca. 1,9 Jahre entspricht.
Das 3. Keplersche Planetengesetz besagt, dass das Verhältnis der dritten Potenz der großeren Halbachse eines Planeten zu der Quadratur seiner Umlaufzeit um die Sonne für alle Planeten konstant ist.
Johannes Kepler war ein deutscher Astronom, Mathematiker und Astrologe im 17. Jahrhundert, der für seine Gesetze der Planetenbewegung bekannt ist, die als die Keplerschen Gesetze bekannt sind.
Die größere Halbachse ist der größere Radius eines elliptischen Planetenbahns. Es ist die Entfernung vom Zentrum der Ellipse bis zu den am weitesten entfernten Punkten auf der Ellipse.
Das 3. Keplersche Gesetz legt fest, dass Planeten, die sich weiter von der Sonne entfernt befinden, eine längere Umlaufzeit haben.
Das Wissen um das 3. Keplersche Gesetz hat eine immense Bedeutung in der modernen Astronomie, da es genutzt wird, um die Umlaufzeiten von exoplaneten um ihre eigenen Sterne zu berechnen.
Das 2. Keplersche Gesetz besagt, dass eine Planetenbahnlinie über gleiche Zeiten hinweg gleiche Flächen ausdecken muss, während das 3. Keplersche Gesetz das Verhältnis der Umlaufzeiten und Bahnradien der Planeten definiert.
Ja, das 3. Keplersche Gesetz kann auf jedes Objekt angewendet werden, das sich in einer Umlaufbahn befindet, einschließlich der Sterne in der Milchstraße.
Das Verhältnis im 3. Keplerschen Gesetz ist das Quadrat der Umlaufzeit eines Planeten proportional zur dritten Potenz seiner mittleren Entfernung zur Sonne.
Die Umlaufbahnen der Planeten sind elliptisch, weil sowohl die Gravitationskraft der Sonne als auch die Bewegungsenergie der Planeten dies verursachen.
Nein, das Newtonsche Gravitationsgesetz ist genauer, aber das 3. Keplersche Gesetz liefert einen einfacheren Weg, um die Umlaufzeiten und Bahnen von Himmelskörpern zu berechnen.