Mit Hilfe des Gravitationsgesetzes lässt sich die Kraft bestimmen, die zwei Körper mit einem bestimmten Abstand aufeinander ausüben (das Gravitationsgesetz gilt auch die Anziehung Erde und Mond)
Das Newtonsche Gravitationsgesetz ist eines der wichtigsten Gesetze in der Physik. Dieses Gesetz besagt, dass jeder Massenpunkt auf jeden anderen Massenpunkt mit einer anziehenden Gravitationskraft wirkt. Die Kraft wirkt entlang der Verbindungslinie beider Massenpunkte. Die Gravitationskraft ist dabei proportional zum Produkt beider Massen und umgekehrt proportional zum Quadrat des Abstandes beider Massen.
Nachfolgend leiten wir das Newtonsche Gravitationsgesetz her und betrachten, welche Bedeutung das Newtonsche Gravitationsgesetz hat,
Herleitung des Newtonschen Gravitationsgesetzes:
Wie bereits bei den Beweisen zur Gültigkeit der Keplerschen Gesetze, verwenden wir die Zentripetalkraft als Grundlage (stabile Kreisbahn)

Für die Bahngeschwindigkeit auf einer Kreisbahn gilt:
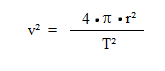
Eingesetzt erhalten wir also:

Durch das 3. Keplersche Gesetz wissen wir: T² : r³ = Konstante (bezeichnen wir sie mit “C”) => T² = C · r³
Wiederrum eingesetzt erhalten wir folgende Gleichung:

Gekürtzt erhalten wir also folgende Gleichung

Nun haben wir die Formel für die Zentripetalkraft bestimmt. Diese Kraft entspricht betragsmäßig der Gravitationskraft. Nun berechnen wir die Gravitationskraft am Beispiel Erde-Sonne.
Damit erhalten wir das Newtonsche Gravitationsgesetz:

Das allgemeine Newtonsche Gravitationsgesetz:

Die Bedeutung des Newtonschen Gravitationsgesetzes
Wie wir gelernt haben, besagt das Newtonsche Gravitationsgesetz, dass zwei Massen (die sich Abstand r zueinander befinden), sich gegenseitig mit einer Gravitationskraft F anziehen. Mit Hilfe des Newtonschen Gesetzes kann man also die Gravitationskraft zwischen zwei Körpern wirken,
Allerdings kann man mit Hilfe des Newtonschen Gravitationsgesetzes auch die Masse der Erde bestimmen. Dazu nehmen wir die Erde mit der Masse m(e) und einen Apfel mit der Masse m(ap)
Gemäß den physikalischen Gesetzen zieht die Erde den Körper (Apfel) mit der Gravitationskraft F an. Allgemein ist aber auch eine Kraft definiert als Masse multipliziert mit der Beschleunigung (F = m·a). Die Beschleunigung lässt sich relativ einfach ermitteln (freier Fall, man lässt den Apfel zu Boden fallen und ermittelt Zeit und Strecke). Daraus ermittelt sich die (Gravitations)beschleunigung auf der Erde mit a bzw. g = 9,81 m/s² .

Setzen wird die bekannten Werte ein:
Gravitationskonstante G = 6,6742 · 10-11 m³/kg*s²
Erdbeschlunigung a = 9,81 m/s²
Erdradius r = ca. 6.370 km (Abstand zum Massenmittelpunkt)
Erhält man für die Masse der Erde ungefähr = 5,96 · 1024 kg
Hinweis: Diese Bestimmung der Erdemasse ist natürlich stark vereinfacht, so ist die Erde keine Kugel (abweichender Erdradius je nach Ort). Für eine grobe Abschätzung der Erdmasse ist das Newtonsche Gravitationsgesetz aber vollkommen ausreichend.
Das Newtonsche Gravitationsgesetz, auch Gesetz der universellen Gravitation genannt, besagt, dass jeder Massepunkt jeden anderen Massepunkt mit einer Kraft anzieht, die direkt proportional zur Masse beider Punkte und umgekehrt proportional zum Quadrat des Abstands zwischen ihnen ist.
Das Gesetz wurde von Sir Isaac Newton formulierte und im Jahr 1687 in seinem Werk Mathematische Prinzipien der Naturlehre veröffentlicht.
Das Newton’sche Gravitationsgesetz wird mathematisch ausgedrückt als F = G * (m1*m2)/r², wobei F die Gravitationskraft, G die Gravitationskonstante, m1 und m2 die Massen der beiden Körper und r der Abstand zwischen den Massenmittelpunkten ist.
Die Gravitationskonstante (G) ist eine physikalische Konstante, die in der Formel des Gravitationsgesetzes vorkommt. Sie hat einen Wert von etwa 6,674*10^-11 N(m/kg)².
Das Gravitationsgesetz besagt, dass die Gravitationskraft direkt proportional zur Masse der beteiligten Objekte ist und umgekehrt proportional zum Quadrat des Abstands zwischen ihren Mittelpunkten.
Die Masse ist eine Eigenschaft eines Körpers und bleibt unabhängig von seiner Position im Raum gleich. Das Gewicht hingegen ist die Kraft, mit der ein Körper aufgrund der Gravitation auf eine Unterlage oder eine Aufhängung drückt, und kann sich je nach Position im Gravitationsfeld ändern.
Das Newtonsche Gravitationsgesetz ist eine gut etablierte und bewährte Theorie, kann aber bei extrem großen Massen, bei extrem kleinen Distanzen oder bei sehr hohen Geschwindigkeiten ungenau werden und wird dann durch die allgemeine Relativitätstheorie von Einstein ersetzt.
Das Newton’sche Gravitationsgesetz ist im Grunde genommen ein spezifischer Ausdruck für das Gesetz der Schwerkraft. Es erklärt, wie die Gravitation zwischen zwei Körpern funktioniert, die durch eine bestimmte Entfernung getrennt sind.
Das Prinzip der Überlagerung besagt, dass wenn ein Körper von mehreren anderen Körpern angezogen wird, die resultierende Gravitationskraft die Vektor-Summe ern Einzelkräfte ist.
Das Newtonsche Gravitationsgesetz wird als universell bezeichnet, weil es auf alle Körper im Universum angewendet werden kann, unabhängig von ihrer Masse und ihrem Abstand.