Die Sinus- und die Cosinusfunktion

Die Sinus- und die Cosinusfunktion gehören zu den sogenannten trigonometrischen Funktionen. In der Mathematik werden Sinus- und Cosinusfunktion verwendet, um alle mathematischen Größen in einem Dreieck zu bestimmen. In allen (anderen) naturwissenschaftlichen Fächern spielen die Sinus- und Cosinusfunktion ebenfalls eine wichtige Rolle. Betrachten wir beispielsweise die Bewegung einer harmonischen Schwingung (Feder mit einem Gewicht, das ausgelenkt wird) oder das Verhalten von Wechselspannung. Diese beiden physikalischen Phänomene lassen sich mithilfe der Sinus bzw. Cosinusfunktion beschreiben. Sowohl die Sinus- als auch die Cosinusfunktion lassen sich ineinander umwandeln

Die Sinus- und Cosinusfunktion

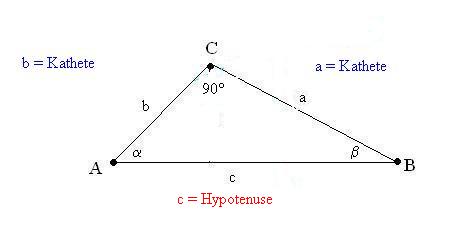
Wie eingangs erwähnt, gehören die Sinus- und Cosinusfunktion zu den trigonometrischen Funktionen. Da die Sinus- und Cosinusfunktion sich auf Winkel in einem Dreieck beziehen, werden die Sinus- und die Cosinusfunktion als Winkelfunktionen bezeichnet. Wie aus der Geometrie bekannt, gibt es in einem Dreieck eine Hypotenuse und zwei Katheten (eine Ankathete und Gegenkathete) und einen Winkel, der zwei “Seiten” des Dreiecks einschließt. Die Sinus und die Cosinusfunktion gelten aber nur in rechtwinkligen Dreiecken. Die Winkelfunktionen Sinus und Cosinus repräsentieren dabei das Verhältnis von Kathete zu Hypotenuse.

Sinus- und Cosinusfunktion

Trigonometrische Funktionen:

• sin (Winkel) = Gegenkathete : Hypotenuse
• cos (Winkel) = Ankathete : Hypotenuse

Die Hypotenuse ist die längste Seite und dem rechten Winkel gegenüber. Die anderen beiden Seiten im Dreieck werden als Katheten bezeichnet. Zur Unterscheidung, ob An- oder Gegenkathete muss man einen bestimmten Winkel betrachten. Die Ankathete ist dabei die Kathete, die an dem Winkel anliegt, die Gegenkathete ist die Kathete, die dem Winkel gegenüberliegt

Beispiel: Betrachten wir den Winkel “Alpha”, so ist die Seite c die Hypotenuse, die Seite (Kathete) b liegt am Winkel Alpha an und ist deshalb die Ankathete und somit die Seite a die Gegenkathete => sin (Alpha) = a : c

Betrachten wir uns nun die Auftragung einer Sinus- bzw. Cosinus-Funktion in Abhängigkeit des Winkels.

Sinus- und Cosinusfunktion

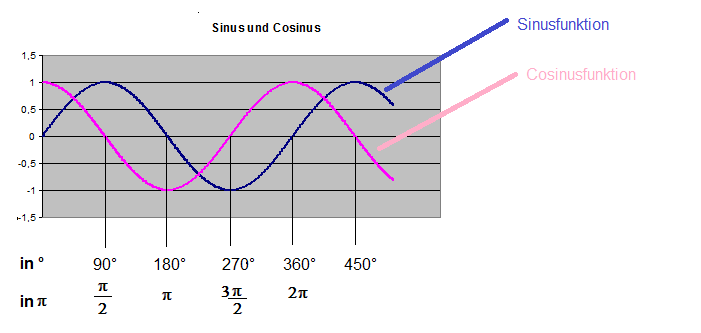
Wie wir anhand des Graphen der Sinus- und der Cosinus-Funkion sehen, haben beide Funktionen (sowohl Sinus als auch Cosinus)

• den gleichen Wertebereich, nämlich das Intervall [-1,1]
• den gleichen Definitionsbereich, nämlich R (alle reellen Zahlen)
• beide Funktionen haben unendlich viele Nullstellen
• der Graph beider Funktionen wiederholt sich in periodischen Abständen (Periode 2π)

Der Unterschied beider Funktionen liegt in der Symmetrie, die Sinusfunktion ist punktsymmetrisch zum Ursprung, während die Cosinusfunktion achsensymmetrisch zur y-Achse ist. Darüber hinaus kann man aus der Abbildung den Zusammenhang zwischen der Sinus- und der Cosinusfunktion erkennen. Verschiebt man den Graphen der Sinusfunktion in -x-Richtung um 90° bzw. um π/2,so ist diese Funktion deckungsgleich mit der Cosinusfunktion. Verschiebt man den Graphen der Cosinusfunktion in x-Richtung um 90° bzw. um π/2,so ist diese Funktion deckungsgleich mit der Sinusfunktion.

Rechenregeln mit Sinus- und Cosinusfunktionen

Aus den oben erwähnten Beziehungen zwischen Sinus und Cosinus leiten sich auch die entsprechenden Regeln ab:

• cos(-x) = cos(x)
• sin(-x) = – sin(x)
• sin(x + y) = sin(x) ·cos(y) + cos(x)· sin(y)
• cos(x + y) = cos(x) ·cos(y) – sin(x)· sin(y)
• sin² (x) + cos²(x) = 1
• sin(2x) = sin(x + x) = 2 sin(x) cos(x)
• cos(2x) = cos(x + x) = cos²(x) – sin²(x)

Die Sinus- und die Cosinusfunktion – Testfragen/-aufgaben

1. Was beschreibt die Sinusfunktion?

Die Sinusfunktion beschreibt die Höhe eines Punktes im Kreis, wenn Sie den Radius und den Winkel, von einer Linie ausgehend (die als 0 Grad betrachtet wird), kennen.

2. Erkläre den Begriff ‘Amplitude’ im Bezug auf eine Sinus- oder Cosinusfunktion.

Die Amplitude einer Sinus- oder Cosinusfunktion ist der maximale Abstand der Funktion von seiner Mitte die in diesem Fall 0 ist.

3. Wie hängen der Sinus und der Cosinus eines Winkels zusammen?

Sinus und Cosinus sind komplementär zueinander; sie sind die Längenverhältnisse im rechtwinkligen Dreieck. Sie verändern sich synchron, sind aber zueinander verschoben.

4. Was passiert mit den Werten der Sinus- und Cosinusfunktionen, wenn der Winkel größer als 90 Grad ist?

Die Werte der Sinus- und Cosinusfunktionen ändern ihre Richtung und können negativ werden, wenn der Winkel größer als 90 Grad ist.

5. Wie bestimmt man den Sinus und den Cosinus eines Winkels in einem rechtwinkligen Dreieck?

Der Sinus eines Winkels in einem rechtwinkligen Dreieck ist das Verhältnis der Länge der gegenüberliegenden Seite zur Länge der Hypotenuse. Der Cosinus ist das Verhältnis der Länge der angrenzenden Seite zur Länge der Hypotenuse.

6. Wie sieht die grafische Darstellung von Sinus- und Cosinusfunktionen aus?

Sinus- und Cosinusfunktionen sind wellenförmige Linien, die sich um die x-Achse schwingen. Der Hauptunterschied besteht darin, dass die Sinusfunktion bei 0 beginnt und die Cosinusfunktion bei 1.

7. Beschreibe, was die Periode einer Sinus- oder Cosinusfunktion ist.

Die Periode einer Sinus- oder Cosinusfunktion ist der Abstand zwischen zwei Punkten, an dem die Funktion anfängt, sich zu wiederholen. Das ist 2𝜋.

8. Welche besonderen Werte sollte man für Sinus- und Cosinusfunktionen auswendig wissen?

Es ist hilfreich, die Sinus- und Cosinuswerte für die Winkel 0°, 30°, 45°, 60° und 90° zu kennen, sowohl in Grad als auch in Rad.

9. Was sagt der Satz von Pythagoras über Sinus- und Cosinusfunktionen aus?

Der Satz von Pythagoras besagt, dass im rechtwinkligen Dreieck das Quadrat des Sinus plus das Quadrat des Cosinus für jeden Winkel immer gleich 1 ist.

10. Welche Veränderungen an der Funktion bewirken Änderungen in der Amplitude, Phase und Frequenz?

Änderungen an der Amplitude verändern die Höhe der Wellen, Änderungen an der Phase verschieben die Welle horizontal und Änderungen an der Frequenz ändern die Geschwindigkeit, mit der die Welle schwingt.