Wie der Name “Redoxtitration” schon sagt, gehört die Redoxtitration zur “Gattung” der Titrationen. Die Titration kennen wir bereits durch die Säure-Base-Titration, einem analytischen Messverfahren, um die Konzentration bzw Stoffmenge einer unbekannten Säure oder Base zu bestimmen. Dabei wird der Säure (bzw. Base) unbekannter Konzentration (= Titrant) eine Base (bzw. Säure) bekannter Konzentration (= Titrator) zugegeben. Aus dem zugegebenen Volumen von Titrator kann die Stoffmenge des Titranten ermittelt werden. Analog dazu kann bei einer Redoxtitration die Konzentration eines Reduktionsmittels (bzw. Oxidationsmittels) durch Zugabe eines Oxidationsmittels (bzw. Reduktionsmittels) genau bestimmt werden. Die Redoxtitration beruht auf denselben Prinzipien wie eine Säure-Base-Titration. Unterschiede gibt es nur bei der Verwendung der zu untersuchenden Stoffe. Bei einer Säure-Base-Titration wird ein Protonendonator bzw. akzeptor titriert, bei der Redoxtitration wird ein Elektronendonator bzw. akzeptor titriert.
Die Redoxtitration als analytische Messmethode:
Wie bereits erwähnt, dient die Redoxtitration dazu, eine Konzentration eines (unbekannten) Stoffes durch Titration zu ermitteln. Im Unterschied zu anderen Titrationsmethoden (wie beispielsweise die Säure-Base-Titration) werden Stoffe titriert, die sich oxidieren oder reduzieren lassen.
Allgemein lässt sich für eine Redoxtitration folgende Reaktionsgleichung angeben:
Während der Redoxreaktion findet eine Elektronenübertragung zwischen Oxidations- und Reduktionsmittel statt. Daher handelt es sich (entsprechend der Säure-Base-Titration) um korrespondierende Paare, so bilden Reduktionsmittel1 und Oxidationsmittel1 ein korrespondierendes Paar. Ohne nun tief in die Redoxchemie einzutauchen, findet eine Elektronenübertragung bei der Redoxreaktion immer vom “Stoff” mit dem niedrigeren Potential zum “Stoff” mit dem höheren Potential (d. h. Elektronen fließen immer vom niedrigeren zum höheren Potential, siehe Kapitel “elektrochemische Spannungsreihe). Wobei auch hier erwähnt werden sollte, dass eine Redoxtitration nur zwischen einem Reduktionsmittel und einem Oxidationsmittel stattfindet. So findet beispielsweise keine Elektronenübertragungsreaktion zwischen zwei Oxidationsmitteln statt, auch wenn diese unterschiedliche Potentiale aufweisen.
Eine Titration muss genau sein, der Titrant soll möglichst wenig Nebenreaktionen ermöglichen und in Lösung stabil sein. Ausserdem muss der Titrant bzw. Titrator bei der Redoxreaktion auch über ein entsprechendes elektrochemisches Potential verfügen, um einen anderen Stoff zu reduzieren bzw. oxidieren (was der häufigste Fall bei Redoxtitrationen ist). Im Rahmen der analytischen Chemie an Schulen und Hochschulen haben sich vier “Redoxtitrationen” durchgesetzt
Im Gegensatz zur Säure-Base-Titration, bei der der sogenannte Äquivalenzpunkt nur durch einen geeigneten Indikator angezeigt werden kann, ist es bei der Redoxtitration möglich, den Äquivalenzpunkt durch sogenannte Eigenindikation zu erkennen (=> Farbumschlag)
Die Methode der Eigenindikation wird vor allem in der Manganometrie (Titration mit Kaliumpermanganat) verwendet, weshalb die Manganometrie auch ein Standardversuch an Schulen und Hochschulen ist. Die Eigenindikation basiert darauf, dass es sich bei dem Titrant um eine farbige Lösung handelt und dessen reduzierte oder oxidierte Form farblos ist bzw. eine andere Farbe aufweist. Titriert man die violette Kaliumpermanagnatlösung, so reagiert dieser Titrator mit dem Titrant, wobei Permanganat zu Mn(II)-Ionen reagiert. Daher kann man den Umschlagpunkt der Redoxtitration erkennen, sobald der Titrant mit Permanganat vollständig reagiert hat, findet beim nächsten Hinzutropfen der Permanganatlösung keine Redoxreaktion mehr statt und die Lösung bleibt violett gefärbt.
Andere Redoxtitrationen basieren auf einem Farbumschlag eines Indikators am Äquivalenzpunkt (wie bei einer Säure-Base-Titration). In diesem Fall werden die Indikatoren als Redoxindikator bezeichnet. Redoxindikatoren beruhen darauf, dass diese Indikatoren selbst oxidiert bzw. reduziert werden können (aber erst, wenn der Titrant vollständig oxidiert bzw. reduziert worden ist). Der bekannteste Redoxindikator ist Ferroin.
Ein Beispiel einer “Mischung” beider Methoden ist die Iodometrie. Bei einer Iodlösung handelt es sich um eine farbige Lösung (je nach Verdünnung gelb gefärbt). Bei der Iodometrie gibt man aber zusätzlich einen “Indikator” dazu, um eine deutlichere Färbung zu erreichen. Im Fall der Iodometrie gibt man Stärke zu der Lösung des Titranten dazu. Befindet sich (überschüssiges) Iod in der Lösung bildet sich ein blauer Stärke-Iod-Komplex, der durch seine intensive Färbung als Indikator bestens geeignet ist.
Die Redoxtitration ist aber nicht nur ein Messverfahren, dass man an Schulen und Hochschulen einsetzt, die Redoxtitration wird auch standardmäßig in industriellen Laboren eingesetzt. Allerdings verwendet man hier keinen Redoxindikator oder die Eigenindikation, sondern misst den Äquivalenzpunkt mithilfe potentiometrischer Methoden. Dabei wird während der Reaktion die Potentialdifferenz in Abhängigkeit des Volumens an zugegebenen Titrator aufgezeichnet. Es entsteht hierbei eine Titrationskurve, die mit einer Säure-Base-Titrationskurve vergleichbar ist. Allerdings stellt die y-Achse nicht den pH-Wert der Lösung dar, sondern die elektrochemische Potentialdifferenz.
Bei der Manganometrie verwendet man in der Regel Kaliumpermanganat als Titrator (dies wird auch als direkte Titration bezeichnet). Wie eingangs erwähnt, handelt es sich bei der Kaliumpermanganatlösung um eine violette Lösung. Tropft man nun den Titrator zu einer geeigneten Lösung (im Rahmen von Praktika wird in der Regel als Titrant eine Eisen(II)-Lösung gewählt), so verschwindet die Farbe der zugetropften Kaliumpermanganatlösung. Dies resultiert aus der Reaktion des Permanganats mit den Eisenionen. Diese Reaktion verläuft bis zum Äquivalenzpunkt (an dem alle Eisen(II)-Ionen reagiert haben). Tropft man nun weiteres Kaliumpermanganat hinzu, findet keine Reaktion mehr statt und die violette Färbung der Kaliumpermagnatlösung bleibt erhalten (durch diese Farbindikation kann der Äquivalenzpunkt “mit dem Auge” beobachtet bzw. bestimmt werden). Neben diesem klassischen Verfahren gibt es auch die inverse Titration. Hier verwendet man als Titrant Kaliumpermanganat und als Titrator beispielsweise die Eisen(II)-Lösung. In diesem Fall bleibt die Farbe des Kaliumpermanganats bis zum Äquivalenzpunkt erhalten und wird durch überschüssige Eisen(II)-Lösung komplett zu Mn(II)-Ionen umgesetzt, wodurch die violette Lösung entfärbt wird.
Auswertung
Bei der direkten Manganometrie wird eine Eisen(II)-Lösung (unbekannter Konzentration, bekanntes Volumen) mit einer Kaliumpermanganatlösung (bekannte Konzentration) bis zum Äquivalenzpunkt titriert. Der Äquivalenzpunkt wird dabei durch eine “anhaltende” schwache violette Färbung der farblosen (bis leicht gelben) Eisenlösung angezeigt. Nun wird das zugegebene Volumen an Titrator (Kaliumpermanganat) abgelesen, typischerweise an einer Bürette.
Analog zur Berechnung des Äquivalenzpunktes bei der Säure-Base-Titration beruht auch die Redoxtitration darauf,, dass am Äquivalenzpunkt die Stoffmengen von Titrant und zugegebenen Titrator äquivalent sind. Bei der Säure-Base-Titration hat man die Äquivalenz anhand der übertragenen Protonen ermittelt, bei der Redoxtitration bezieht sich die Äquivalenz auf die Zahl der übertragenen Elektronen.
Im ersten Schritt wird daher immer die “Äquivalenzmenge” bestimmt (analog zu einer Säure-Base-Titration). Dazu stellen wir im ersten Schritt die zugehörige Redoxtitration auf.
Das Stoffmengenverhältnis zwischen Oxidationsmittel (Permanagnat) und dem Reduktionsmittel (Eisen(II)) beträgt 1 : 5. Das bedeutet, dass am Äquivalenzpunkt gilt:
Über die Beziehung “Stoffmenge n” = “Konzentration c” · “Volumen V” kann nun die Konzentration der Eisenlösung ermittelt werden.
Potentiometische Messung der Redoxtitration
Wie oben beschrieben, basiert die potentiometrische Messung der Redoxtritartion auf Basis der Messung des elektrochemischen Potentials zweier Halbzellen (MnO4– und Mn2+) bzw. ( Fe2+ und Fe3+). Zur Bestimmung einer Potentialdifferenz zweier Halbzellen wird die sogenannte Nernst-Gleichung verwendet:
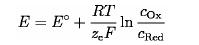
Zur Berechnung verwenden wir anschließend: ∆E = E2 – E1 (Zuordnung E1 und E2 entsprechend den Vorgaben der IUPAC)
Betrachten wir nun die Redoxtitration (Manganometrie),
Dies ergibt folgendes Diagramm:

Titrationskurve – Redoxtitration
Die Redoxreaktion ist eine chemische Reaktion, bei der eine Oxidation und eine Reduktion gleichzeitig stattfinden. Dabei werden Elektronen von einem Atom, Ion oder Molekül auf ein anderes übertragen.
Redoxtitration ist eine Methode in der analytischen Chemie, die verwendet wird, um die Konzentration eines unbekannten Oxidationsmittels oder Reduktionsmittels zu bestimmen.
Der Indikator bei der Redoxtitration zeigt den Endpunkt der Titration an, d.h. den Punkt, an dem alle Verbindungen, welche die Redoxreaktion auslösen, verbraucht sind.
Ein Oxidationsmittel ist eine Substanz, die Elektronen aus anderen chemischen Substanzen entzieht, wodurch sie selbst reduziert wird. Ein Reduktionsmittel gibt Elektronen an andere chemische Substanzen ab, wodurch es selbst oxidiert wird.
Die Äquivalenzpunkt-Methode dient dazu, die Konzentration des analysierten Stoffes zu bestimmen. Sie bezeichnet den Punkt in der Titration, an dem das genaue stöchiometrische Verhältnis erreicht ist.
Die Normalität ist ein Maß für die Konzentration von Protonen im Lösungsmittel. Sie wird oft in der Säure-Base-Titration und der Redox-Titration verwendet, um den Äquivalenzpunkt zu bestimmen.>
Ja, eine Redoxtitration kann dazu verwendet werden, die Reinheit eines Stoffes zu bestimmen. Durch Titration kann die genaue Konzentration eines Stoffes in einer Probe festgestellt werden, was auf seine Reinheit schließen lässt.
Die Unterscheidung ist wichtig, weil starke Oxidationsmittel in der Lage sind, mehr Elektronen zu entfernen und so stärkere Redoxreaktionen auszulösen als schwache Oxidationsmittel.
Ja, Redoxtitrationen können in der industriellen Analyse verwendet werden, zum Beispiel zur Bestimmung der Konzentration von Eisen in Erz oder von Vitamin C in Lebensmitteln.
Das benötigte Volumen wird durch sorgfältige Dosierung der Titrationslösung und Beobachtung der Farbänderung des Indikators ermittelt. Sobald der notwendige Äquivalenzpunkt erreicht ist, ändert die Lösung ihre Farbe und das Volumen der Titrationslösung kann abgelesen werden.