Ausgewählte Stammfunktionen bzw. Lösungen von Differentialgleichungen

Das Lösen von Differentialgleichungen ist eines der wichtigsten Kapitel nicht nur in der Mathematik, sondern auch in den anderen Naturwissenschaften.
Grundsätzlich unterscheidet man nach gewöhnlicher und partieller Differentialgleichung, wobei die Zahl der auftretenden Variablen zur Unterscheidung verwendet wird:

• Gewöhnliche Differentialgleichung: die gesuchte Funktion hängt nur von einer Variablen ab (y’ = f(x))
• Partielle Differentialgleichung: die gesuchte Funktion hängt von mehreren Funktionen bzw. Variablen ab (y’ = f(x)·g(y))

Daneben existieren noch die Bernoulli-Differentialgleichungen (y’ = f(x)y + h(x)yr) und die Ricatti-Differentialgleichungen (y’ = f(x) + g(x)y + h(x)y)

Lösungsverfahren

Die Lösung einer Differentialgleichung kann im Allgemeinen nicht durch die Gleichung selbst eindeutig bestimmt werden, sondern benötigt zusätzlich noch weitere Anfangs- oder Randwerte zu exakten Bestimmung. Daher ist es nicht möglich, eine allgemein gültige Lösungsmethodik anzugeben. Nur für gewöhnliche, integrable Differentialgleichungen existiert ein allgemeines Lösungsverfahren.
Folgende Lösungsverfahren sind möglich:

• Für gewöhnliche Differentialgleichungen benutzt man die Umkehrung des Differenzierens, in dem man die Stammfunktion aufsucht und so die Differentialgleichung integriert. Die Lösungsfunktion ist dann einfach die Stammfunktion der Differentialgleichung. Beispiel: f´(x) = 4, dann ist die Stammfunktion F(x) = 4x + C und somit die Lösung der Differentialgleichung.
• Partielle Differentialgleichungen werden in erster Linie durch Trennung der Variablen und spätere Integration gelöst.

Ausgewählte Stammfunktionen

Nachfolgend findet sich ein Überlick über die wichtigsten Stammfunktionen, die zur Lösung von partiellen Differentialgleichungen immer wieder benötigt werden.

Mithilfe der Kenntnis der Stammfunktionen lässen sich viele (partielle) Differentialgleichungen lösen.
Zur Wiederholung: Lösungsverfahren von partiellen Differentialgleichungen

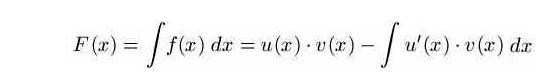
Lösungsverfahren von partiellen Differentialgleichungen

Ausgewählte Stammfunktionen bzw. Lösungen von Differentialgleichungen – Testfragen/-aufgaben

1. Definieren Sie den Begriff “Stammfunktion”.

Die Stammfunktion ist eine unbestimmte Integralfunktion. Sie ist eine umgekehrte Funktion zur Ableitungsoperation in der Differentialrechnung. Jede Differentiale einer Funktion führt zur Stammfunktion rückwärts.

2. Was ist eine Differentialgleichung?

Eine Differentialgleichung ist eine Gleichung, die die Ableitungen einer unbekannten Funktion beinhaltet.

3. Beschreiben Sie die Methode, um eine einfache Differentialgleichung zu lösen.

Um eine einfache Differentialgleichung zu lösen, müssen wir die Funktion finden, deren Ableitungen die Gleichung befriedigen, indem wir die Stammfunktion bestimmen.

4. Gibt es mehrere Stammfunktionen einer Funktion? Erklären Sie Ihre Antwort.

Ja, es gibt unendlich viele Stammfunktionen zu einer gegebenen Funktion, da die Stammfunktion bis auf eine Konstante eindeutig ist.

5. Welche Rolle spielt die Konstante in der Stammfunktion?

Die Konstante repräsentiert die Unbestimmtheit der Stammfunktion. Sie erfasst die ‘verschobenen’ Kopien der Stammfunktion entlang der y-Achse.

6. Was ist ein unabhängiges und was ist ein abhängiges Variable in einer Differentialgleichung?

In einer Differentialgleichung ist die unabhängige Variable diejenige, die sich frei ändern kann, während die abhängige Variable diejenige ist, die sich in Abhängigkeit von der unabhängigen Variable ändert.

7. Definieren Sie den Begriff ‘partikuläre Lösung’ im Kontext der Differentialgleichungen.

Eine partikuläre Lösung ist eine spezifische Lösung der Differentialgleichung, die durch Einsetzen der Anfangsbedingungen oder Randbedingungen erhalten wurde.

8. Was ist die Grundidee hinter der Integralrechnung?

Die Grundidee hinter der Integralrechnung ist die Berechnung der Fläche unter einer Kurve.

9. Nennen Sie zwei Anwendungen der Differential- und Integralrechnung.

Zwei Anwendungen der Differential- und Integralrechnung können Physische Phänomene, wie die Geschwindigkeit eines sich bewegenden Objekts und die Berechnung der Fläche unter einer Kurve, sein.

10. Beschreiben Sie, worin der Unterschied zwischen einer Differentialgleichung erster und zweiter Ordnung besteht.

Eine Differentialgleichung erster Ordnung enthält nur die erste Ableitung der unbekannten Funktion, während eine Differentialgleichung zweiter Ordnung sowohl die erste als auch die zweite Ableitung der unbekannten Funktion enthält.