Das Lösen von Differentialgleichungen ist eines der wichtigsten Kapitel nicht nur in der Mathematik, sondern auch in den anderen Naturwissenschaften.
Grundsätzlich unterscheidet man nach gewöhnlicher und partieller Differentialgleichung, wobei die Zahl der auftretenden Variablen zur Unterscheidung verwendet wird:
Daneben existieren noch die Bernoulli-Differentialgleichungen (y’ = f(x)y + h(x)yr) und die Ricatti-Differentialgleichungen (y’ = f(x) + g(x)y + h(x)y)
Die Lösung einer Differentialgleichung kann im Allgemeinen nicht durch die Gleichung selbst eindeutig bestimmt werden, sondern benötigt zusätzlich noch weitere Anfangs- oder Randwerte zu exakten Bestimmung. Daher ist es nicht möglich, eine allgemein gültige Lösungsmethodik anzugeben. Nur für gewöhnliche, integrable Differentialgleichungen existiert ein allgemeines Lösungsverfahren.
Folgende Lösungsverfahren sind möglich:
Wichtig ist, dass aus der Lösung der Differentialgleichung immer gilt, dass die Lösungsmenge einer Differentialgleichung im allgemeinen eine Funktionenschar ist (durch die Konstante C). Ist nun eine genau definierte Funktion als Lösung gesucht, so reicht die Vorgabe der Differentialgleichung nicht aus, sondern dazu benötigt man noch einen Anfangs- oder Randwert. Zur Lösung dieses Problems kann man auf einige Regeln zurückgreifen:
Eine Differentialgleichung bzw. deren Lösung ist im Allgemeinen eine Funktion und bildet damit einen Graphen ab. Jeder Punkt auf dem Graphen kann zugeordnet werden. Mit einem gegebenen Anfangswert kann nun die eindeutige Lösung berechnet werden um so aus der Fülle der Lösungen einer Differentialgleichung eine bestimmte Lösung auszuwählen (oft als Anfangswertproblem (AWP), Anfangswertaufgabe (AWA) oder Cauchy-Problem bezeichnet).
Beispiel: y´(x) = x
Die Lösung dieser Differentialgleichung (Stammfunktion) ist F(x) = 0,5·x² + C (C ist eine Konstante).
Nun kann man sich einige Lösungsfunktionen einmal betrachten:
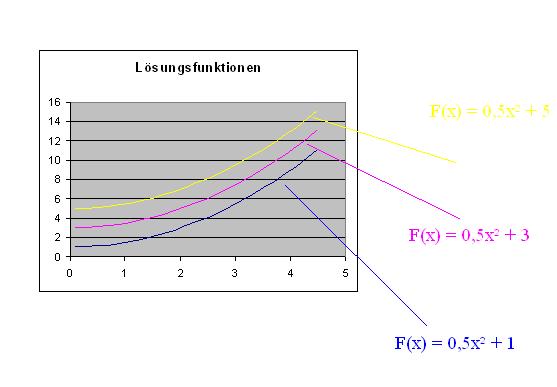
Lösungen der Differentialgleichung
All diese Funktionen sind Lösungen der Differentialgleichung. Sucht man aber einen bestimmten Punkt, so ist nur eine der Lösungen exakt. Soll der Punkt (4,5 / 11,125) auf dem Graphen liegen, so kommt als Lösung der Differentialgleichung nur F(x) = 0,5x² + 1 in Frage.
Wie löst man nun das Anfangswertproblem?
Ein Anfangswertproblem wird immer folgendermaßen gelöst:
Zuerst wird immer die Differentialgleichung gelöst. Dabei taucht in der Lösung immer eine Integrationskonstante (meist als “C” bezeichnet) auf. Die exakte Lösung kann mithilfe einer Anfangsbedingung bestimmt werden (Anfangsbedingung wird in die allgemeine Lösung der DGL eingesetzt) und erhält so eine Lösung, die die Anfangsbedingung erfüllt.
Beispiel: Als Lösung traf vorher F(x) = 0,5x² + C auf. Zusätzlich soll als Punkt (der eine Lösung von F(x) ist) P (4,5 / 11,125) vorgegeben sein. Dazu setzt man einfach den Wert in F(x) = y = 0,5x² + C ein und erhält C.
Lösung: 11,125 = 0,5·(4,5)² + C
C = 11,125 – 10,125 = 1
Die exakte Lösung der DGL y´(x) = x stellt somit F(x) = 0,5x² + 1 dar.
Eine Differentialgleichung ist eine Gleichung, die die Ableitung einer unbekannten Funktion enthält. Eine exakte Lösung dieser Gleichung ist eine Funktion, deren Ableitung genau die Gleichung erfüllt.
Die exakte Lösung einer Differentialgleichung kann man bestimmen, indem man die Differentialgleichung löst, sprich, man bestimmt die Funktion, deren Ableitung die gegebene Gleichung erfüllt.
Ein Anfangswertproblem ist ein Problem, bei dem man eine Differentialgleichung zusammen mit einem spezifischen Anfangswert lösen muss.
Der Anfangswert ist wichtig, weil er die spezifische Lösung der Differentialgleichung bestimmt. Es gibt unendlich viele Funktionen, deren Ableitungen die gleiche Differentialgleichung erfüllen, aber nur eine, die den gegebenen Anfangswert erfüllt.
Eine allgemeine Lösung einer Differentialgleichung ist eine Familie von Funktionen, die alle die gleiche Ableitung haben und somit alle die gleiche Differentialgleichung erfüllen.
Die spezielle Lösung unterscheidet sich von der allgemeinen Lösung darin, dass sie zusätzlich einen spezifischen Anfangswert erfüllt.
Die spezielle Lösung einer Differentialgleichung kann man bestimmen, indem man zunächst die allgemeine Lösung findet und diese dann so anpasst, dass sie den gegebenen Anfangswert erfüllt.
Wenn man verschiedene Anfangswerte für die gleiche Differentialgleichung hat, erhält man verschiedene spezielle Lösungen. Jede spezielle Lösung erfüllt den entsprechenden Anfangswert.
Man kann feststellen, ob eine Funktion eine Lösung einer Differentialgleichung ist, indem man ihre Ableitung bestimmt und prüft, ob diese die Gleichung erfüllt.
Nicht jede Differentialgleichung hat eine exakte Lösung, die man in geschlossener Form ausdrücken kann. In diesen Fällen ist es oft erforderlich, numerische Methoden zur Bestimmung der Lösung zu verwenden.