Das Lösen von Differentialgleichungen ist eines der wichtigsten Kapitel nicht nur in der Mathematik, sondern auch in den anderen Naturwissenschaften.
Grundsätzlich unterscheidet man nach gewöhnlicher und partieller Differentialgleichung, wobei die Zahl der auftretenden Variablen zur Unterscheidung verwendet wird:
Daneben existieren noch die Bernoulli-Differentialgleichungen (y’ = f(x)y + h(x)yr) und die Ricatti-Differentialgleichungen (y’ = f(x) + g(x)·y + h(x)y)
Die Lösung einer Differentialgleichung kann im Allgemeinen nicht durch die Gleichung selbst eindeutig bestimmt werden, sondern benötigt zusätzlich noch weitere Anfangs- oder Randwerte zu exakten Bestimmung. Daher ist es nicht möglich, eine allgemein gültige Lösungsmethodik anzugeben. Nur für gewöhnliche, integrable Differentialgleichungen existiert ein allgemeines Lösungsverfahren.
Folgende Lösungsverfahren sind möglich:
Wie oben schon beschrieben, hängt die partielle Differentialgleichung von mehreren Funktionen bzw. Variablen ab. Genauso wie bei den gewöhnlichen Differentialgleichungen gibt es auch hier die Begriffe “homogen” und “inhomogen”. Eine Differentialgleichung heißt homogen, wenn die keine sog. Störfunktion
aufweist (Beispiel: y´(x) + f(x) + g(y) = 0 => homogen). Ist dies jedoch der Fall, nennt man sie inhomogen. Zur Lösung von partiellen Differentialgleichungen kann man auf die Regel der Produktableitung zurückgreifen.
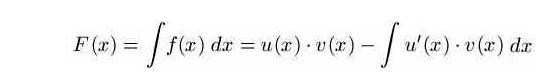
Rückgriff auf die Regel der Produktableitung
Bei “geschicktem” Umwandeln der gegebenen Differentialgleichung in ein u(x) bzw. v(x) kann die partielle Differentialgleichung leicht gelöst werden. Ziel ist es dabei, dass u´(x) eine Zahl ist, und so leicht integriert (Integration von gewöhnlichen Differentialgleichungen) werden kann.
Beispiel:

Lösungsverfahren
Die Lösung einer Differentialgleichung mithilfe der eben gezeigten Verfahren kann im Allgemeinen nicht die Gleichung selbst eindeutig bestimmen (deswegen C = Konstante), sondern benötigt zusätzlich noch weitere Anfangs- oder Randwerte zu exakten Bestimmung.
Unter einer partiellen Differentialgleichung versteht man eine Gleichung, die die Beziehung zwischen einer unbekannten Funktion und ihren partiellen Ableitungen darstellt.
Eine allgemeine partielle Differentialgleichung zweiter Ordnung hat die Form Au_xx + 2Bu_xy + Cu_yy + Du_x + Eu_y + F = 0, wobei u die gesuchte Funktion und A, B, C, D, E und F Funktionen der unabhängigen Variablen sind.
Zwei Arten von partiellen Differentialgleichungen sind lineare und nichtlineare partielle Differentialgleichungen.
Der Unterschied liegt darin, dass bei linearen partiellen Differentialgleichungen die gesuchte Funktion und ihre Ableitungen nur bis zur ersten Potenz auftreten, während bei nichtlinearen partiellen Differentialgleichungen die gesuchte Funktion und ihre Ableitungen auch in höheren Potenzen oder Produktformen auftreten können.
Ein Beispiel für eine lineare partielle Differentialgleichung ist die Wärmeleitungsgleichung.
Es gibt verschiedene Lösungsstrategien für partielle Differentialgleichungen, darunter die Trennung der Variablen, die Methode der Charakteristiken und Numerische Methoden.
Ein Beispiel für eine Lösungsmethode für nichtlineare partielle Differentialgleichungen ist die Methode der Charakteristiken.
Unter der Methode der Trennung der Variablen versteht man eine Lösungsmethode, bei der man annimmt, dass die gesuchte Funktion als Produkt von Funktionen geschrieben werden kann, die jeweils nur von einer der unabhängigen Variablen abhängen.
Ein Anwendungsgebiet für partielle Differentialgleichungen ist die Physik, wo sie beispielsweise in der Wärmeleitung, der Elektrostatik oder der Quantenmechanik vorkommen.
Das Ziel beim Lösen einer partiellen Differentialgleichung ist es, eine Funktion zu finden, die alle in der Gleichung formulierten Bedingungen erfüllt. Oft sucht man eine Lösung, die auch bestimmte Randbedingungen erfüllt.