Die Potenz- und Summenregel für Ableitungen

Ganz einfach gesagt: Die Differentialrechnung untersucht das Steigungsverhalten von (Funktions)Graphen. So kann man auch die Ableitung auf einen Graphen übertragen, die (1.) Ableitung einer Funktion bzw. eines Graphen ist deren Steigungsverhalten (also, wie verändert sich der Graph). Der Sinn von Ableitungen ist in der Regel nicht das Lösen von Gleichungen, sondern Funktion bzw. Graphen charakterisieren zu können (z.B. “Extrempunkte (Hoch- oder Tiefpunkt)”). Die 2. Ableitung gibt an, wie “gekrümmt” die Funktion ist. Weiteren Ableitungen sind für die Charakterisierung der Ausgangsfunktion nicht mehr aussagekräftig bzw. ohne Bedeutung.

Ableitungen werden überall dort verwendet, wo die Änderung einer Größe von der gleichen Größe selbst abhängt.
Beispiele:

• Die Funktion f beschreibt den Ort, dann beschreibt die f´ die Änderung des Ortes und das ist nichts anderes, als die Geschwindigkeit
• Die Funktion f beschreibt die Größe eine Bevölkerung, dann beschreibt f´deren Änderung und das ist nichts anderes als das Bevölkerungswachstum. Allgemein beschreibt die Funktion f eine Größe und f´die Änderungsrate dieser Größe

Wie funktioniert “Differenzieren” (Ableiten)?

Zum Differenzieren von Funktionen kann man die Potenz- (f(x) =a·xⁿ) bzw. Summenregel (f(x) =a·xⁿ+ b·x^m) für einfache Funktionen verwenden. Für schwierigere Fälle benötigt man die Produkt- bzw. Quotientenregel (f(x) = u(x) · v(x)), manchmal auch die Kettenregel (f(x) = (x + b)ⁿ). Daneben gibt es noch einzelne Funktionen, deren Ableitung (Lösung) man auswendig lernen muss.

Anwendung der Potenz- bzw. Summenregel

Wie in der Einleitung beschrieben, ist Potenzregel ist in der Mathematik eine der Grundregeln der Differentialrechnung und dient zum Ableiten von einfachen Funktionen des Types: f(x) =a·xⁿ. Eine Erweiterung der Potenzregel ist die Summenregel (in Verbindung mit der Potenzregel) und lässt sich bei Funktionen des Typs (f(x) =a·xⁿ+ b·x^m) anwenden.

Die der Potenzregel zugrundeliegende Formel ist relativ einfach:

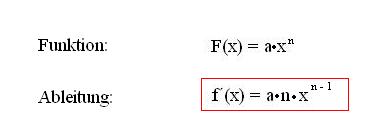
Potenzregel

Eine (Potenz)funktion (f(x) =a·xⁿ) wird mithilfe der Potenzregel abgeleitet (differenziert), indem man den Exponenten z.B.”n” (Hochzahl, die über dem “x” steht”) um eins verringert (n-1) und diese Hochzahl (n) mit der Ausgangsfunktion multipliziert.

Nun kann die Funktion, die differenziert werden soll, mehr Glieder enthalten (z.B. f(x) =a·xⁿ+ b·x^m). Hier kommt nun die Summenregel ins Spiel, die besagt, dass eine Summe (von Funktionsgliedern) so abgeleitet wird, indem man jeden Summanden für sich ableitet und die Ableitungen addiert (in anderen Worten: die Summe aus zwei oder mehreren differenzierbaren Funktionensgliedern kann gliedweise differenziert werden).

F(x) = g(x) + h(x)
f´(x) = g´(x) + h´(x)

Beispiele:

• F(x) = x² => f´(x) = 2x : Der Exponent über dem “x”, die Zahl 2, wird um eins verringert (2 -> 1) und ergibt die neue Funktion (Ableitung), der ehemalige Exponent “2” wird mit der neuen Gleichung multipliziert.

• F(x) = x²ⁿ => f´(x) = 2nx^2n-1

• F(x) = 2x³ + x² => f´(x) = 6x² +2x