Eine Funktion stellt einen Zusammenhang zwischen zwei Elementen her (einer unabhängigen Variable und einer abhängigen Variable). Die Untersuchungen von Funktionen sind wesentlicher Bestandteil der sog. Kurvendiskussion. Ein Untersuchungskriterium einer Funktion ist die Bestimmung von Extremwerten der Funktion. Extremwerte sind beispielsweise das Minimum und das Maximum einer Funktion (eines Graphen)
(Fast) jede Funktion bzw. jede Abbildung in einem Koordinatensystem hat einen “höchsten” Punkt und einen “tiefsten” Punkt. In der Analysis (bzw. der Kurvendiskussion) werden solche Punkte (bzw. Werte) als Hochpunkt (=> Maximum) und Tiefpunkt (=> Minimum) bezeichnet. Diese beiden Punkte werden auch als Extremwerte bezeichnet und lassen sich mit Hilfe der Steigung der Funktion (zeichnerisch und rechnerisch) ermitteln:
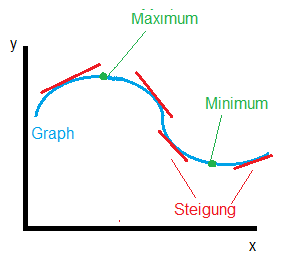
Die Extremwerte einer Funktion
Wie wir in der obigen Abbildung erkennen, lässt sich ein Extremwert (egal ob Hochpunkt oder Tiefpunkt) näherungsweise graphisch ermitteln, die genauen Koordinatenangaben müssen in der Regel rechnerisch ermittelt werden. Und hier hilft uns die 1. Ableitung. Denn die 1. Ableitung einer Funktion ist nichts anders, als die Steigung der Funktion.
Um die Extremwerte der Funktion zu bestimmen, gehen wir nun folgendermaßen vor:
Nun ist die Mathematik “doch” etwas komplizierter, was man aber erst in höheren Klassenstufen lernt, aber hier schon einmal ein Vorgriff:
Unter Extremwerten einer Funktion versteht man die höchsten (maxima) und niedrigsten (minima) Werte, die eine Funktion annimmt. Sie werden durch die Ableitung der Funktion bestimmt.
Die Extremwerte einer Funktion finden Sie, indem Sie die erste Ableitung der Funktion bilden und diese gleich Null setzen. Die Lösungen dieser Gleichung sind die möglichen Extremwerte. Mit Hilfe der zweiten Ableitung können Sie dann bestimmen, ob es sich um ein Maximum oder ein Minimum handelt.
Sie bestimmen, ob ein Extremwert ein Maximum oder ein Minimum ist, indem Sie die zweite Ableitung der Funktion an dieser Stelle berechnen. Ist diese positiv, handelt es sich um ein Minimum, ist sie negativ, um ein Maximum.
Lokale Extremwerte liegen innerhalb eines bestimmten Bereichs einer Funktion und sind dort die höchsten oder niedrigsten Werte. Globale Extremwerte sind hingegen die höchsten oder niedrigsten Werte der gesamten Funktion.
Unter einer Kurvendiskussion versteht man die analytische Untersuchung einer Funktion bezüglich ihrer wichtigsten Eigenschaften wie Nullstellen, Extremstellen, Wendepunkten, Symmetrie, Asymptoten und Verhalten im Unendlichen.
Wendepunkte einer Funktion bestimmen Sie, indem Sie die zweite Ableitung der Funktion bilden und diese gleich Null setzen. Die Lösungen dieser Gleichung sind die möglichen Wendepunkte. Mit Hilfe der dritten Ableitung können Sie dann überprüfen, ob es sich tatsächlich um einen Wendepunkt handelt.
Die Ableitungen einer Funktion spielen eine zentrale Rolle bei der Bestimmung von Wendepunkten und Extremstellen. Die erste Ableitung wird verwendet, um Extremstellen zu finden, während die zweite Ableitung zur Bestimmung von Wendepunkten dient.
Die Symmetrie einer Funktion kann man bestimmen, indem man die Funktion auf gerade oder ungerade Funktionen untersucht. Eine Funktion ist gerade, wenn sich das Vorzeichen nicht ändert, wenn x durch -x ersetzt wird. Sie ist ungerade, wenn sich das Vorzeichen ändert, wenn x durch -x ersetzt wird.
Die Nullstellen einer Funktion sind die x-Werte, für die der Funktionswert gleich null ist. Man findet die Nullstellen, indem man die Funktion gleich null setzt und diese Gleichung nach x auflöst.
An den Stellen, an denen die Ableitung einer Funktion null ist, liegen entweder Extremstellen oder Sattelpunkte vor. Ob es sich um ein Extremum oder einen Sattelpunkt handelt, kann man mit Hilfe der zweiten Ableitung bestimmen.