Monotonieverhalten von Funktionen

Im Kapitel “Ableitung” von Funktion ist bereits erwähnt worden, dass der Hauptzweck von Ableitungen der Charakterisierung von Funktionen bzw. deren Graphen dient. Diese Untersuchungen von Funktionen sind wesentlicher Bestandteil der sog. Kurvendiskussion. Das Ziel dabei ist, die Eigenschaften einer Funktion herauszufinden, ohne diese graphisch lösen zu müssen (also zu zeichnen). Wichtige (zu bestimmende) Eigenschaften sind dabei: Extrempunkte, Wendepunkte, Nullstellen, Krümmungsverhalten und Symmetrie.

Notwendigkeit der Untersuchungen von Funktionen

Die Untersuchung von Funktionen (Kurvendiskussion) ist nicht nur eine elementare mathematische Methode, sondern findet auch außerhalb der Mathematik breite Anwendung, z.B. in der Chemie: der Verlauf einer Reaktion lässt sich beschreiben. Aber nicht nur in den MINT-Fächern stößt man immer wieder auf die Notwendigkeit, Graphen zu untersuchen bzw. zu interpretieren. Bestes Beispiel ist z.B. die Berechnung des Break-Even (in wirtschaftlichen Fächern), oft handelt es sich dabei um komplizierte Funktionen mit deren Hilfe berechnet werden soll, ab welcher Stückzahl man Gewinn macht.

Untersuchungen von Funktionen – Monotonieverhalten

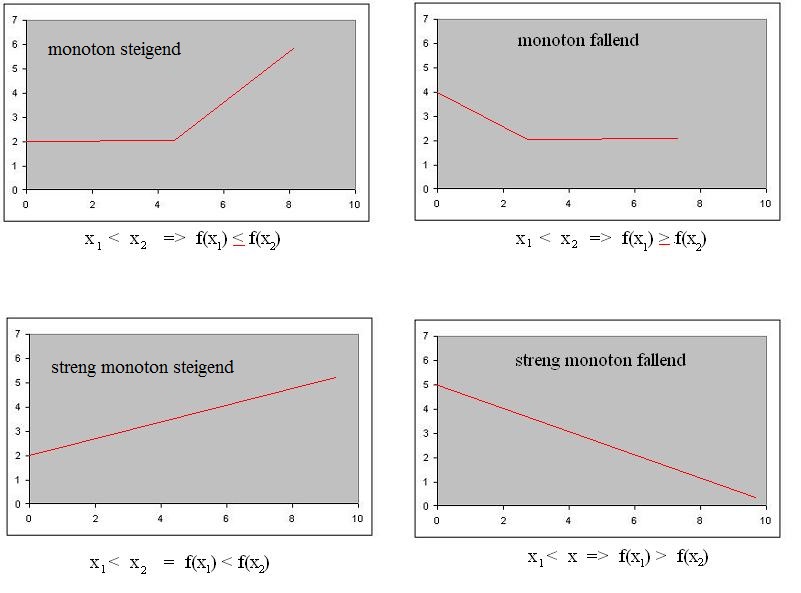
Prinzipiell lässt sich mit Monotonieverhalten einer Funktion der Verlauf des Graphen einer Funktion einfacher beschreiben. Dabei kann man aussagen, ob “die Funktion bzw. der Graph steigt, fällt oder konstant ist”. Steigender Graph bzw. Funktion bedeutet, dass mit zunehmendem x-Wert der zugehörige y-Wert bzw. Funktionswert zunehmen muss (x₁ < x₂ => f(x₁) < f(x₂)) Fallender Graph bedeutet genau das Gegenteil.

Zusätzlich zu monoton fallend bzw. monoton steigend gibt es noch den mathematischen Ausdruck streng monoton fallend bzw. streng monoton steigend.
Streng monoton steigend heißt eine Funktion, die bei wachsendem x-Wert einen immer größeren oder konstanten y-Wert aufweist (der y-Wert wird also niemals kleiner mit steigendem x-Wert). Streng monoton steigend sind also Funktionen, deren y-Wert nur immer größer und niemals konstant wird.

Untersuchungen von Funktionen – Monotonieverhalten

Bestimmung des Monotonieverhaltens

Man bestimmt das Monotonieverhalten einer differenzierbaren Funktion mithilfe ihrer ersten Ableitung.

• Wenn für alle x-Werte gilt: f´(x) > 0, ist die Funktion monoton steigend.

• Wenn für alle x-Werte gilt f´(x) < 0, ist die Funktion monoton fallend.

Wie geht man vor?

anhand des Beispiels: f(x) = 1/3·x³ + x² – 3x

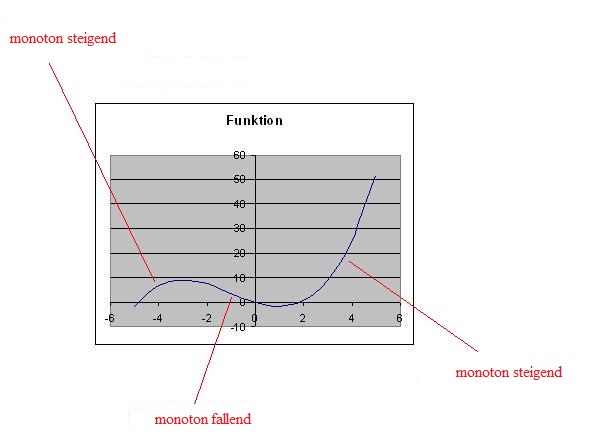
Bestimmung des Monotonieverhaltens

• 1. Schritt: Man leitet die gegebene Funktion ab: f´(x) = x² + 2x -3

• 2. Schritt: man bestimmt die Nullstellen: in unserem Fall (-3/0) und (1/0)

• 3. Schritt: Zerlegung der Funktion in Intervalle: Die Nullstellen trennen dabei die einzelnen Intervalle des Graphen

• 4. Schritt: Nachdem die Funktion in einzelne Intervalle unterteilt ist kann man eine Aussage treffen, ob die Funktion im betrachteten Intervall monoton steigend oder fallend ist (die einfachste Lösung ist “Durchtesten”)

z.B. für Intervall -3 < x < 1. Setzt man z.B x = -2 in f´(x) ein. f´(-2) = (-2)² + 2(-2) -3 = -3 und damit kleiner als 0.

Monotonieverhalten von Funktionen – Testfragen/-aufgaben

1. Was versteht man unter dem Monotonieverhalten einer Funktion?

Unter dem Monotonieverhalten einer Funktion versteht man die Eigenschaft der Funktion, ob sie im gesamten Definitionsbereich oder in bestimmten Intervallen stetig steigt oder fällt. Somit kann eine Funktion monoton steigend, monoton fallend, streng monoton steigend oder streng monoton fallend sein.

2. Was ist eine monoton steigende Funktion?

Eine Funktion heißt monoton steigend, wenn sie mit steigendem x-Wert nicht abnimmt.

3. Was ist eine monoton fallende Funktion?

Eine Funktion heißt monoton fallend, wenn sie mit steigendem x-Wert nicht zunimmt.

4. Wie kann man das Monotonieverhalten einer Funktion bestimmen?

Das Monotonieverhalten einer Funktion kann man durch die Untersuchung der ersten Ableitung bestimmen. Ist die erste Ableitung positiv, so ist die Funktion im betreffenden Interval streng monoton steigend. Ist die erste Ableitung negativ, so ist die Funktion streng monoton fallend.

5. Was bedeutet “streng monoton steigend”?

Eine Funktion heißt streng monoton steigend, wenn sie mit steigendem x-Wert stetig zunimmt.

6. Was bedeutet “streng monoton fallend”?

Eine Funktion heißt streng monoton fallend, wenn sie mit steigendem x-Wert stetig abnimmt.

7. Könnte eine Funktion gleichzeitig monoton steigend und monoton fallend sein?

Nein, eine Funktion kann nicht gleichzeitig monoton steigend und monoton fallend sein.

8. Was ist der Unterschied zwischen einer monotonen und einer streng monotonen Funktion?

Der Unterschied liegt darin, dass eine monotone Funktion nicht unbedingt überall steigt oder fällt, sie kann auch gleichbleiben. Eine streng monotone Funktion hingegen steigt oder fällt überall.

9. Kann das Monotonieverhalten einer Funktion wechseln?

Ja, das Monotonieverhalten einer Funktion kann wechseln. Zum Beispiel, wenn die erste Ableitung ihre Vorzeichen ändert, ändert sich auch das Monotonieverhalten der Funktion.

10. Wie sind Extremstellen einer Funktion mit deren Monotonieverhalten verbunden?

Die Extremstellen einer Funktion entsprechen den Punkten, an denen das Monotonieverhalten wechselt. Sie müssen also entweder Maxima oder Minima sein.